二维非稳态热传导 膏体发动机
一、划分网格:
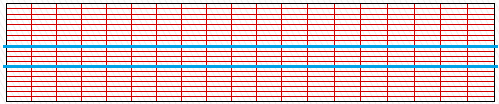
X 方向网格:20;Y 方向网格:20 材料 1:材料 2:材料 1=8:4:8
总网格数量:400
网格尺寸:
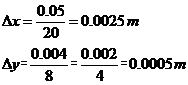
注意有界性条件:方程的各项系数大于 0
显式格式:

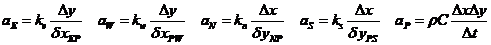
网格时
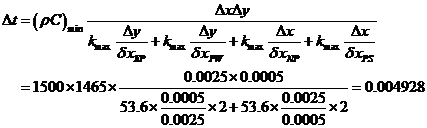
网格时
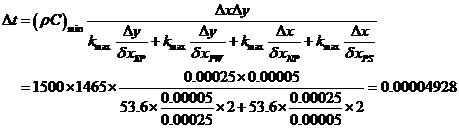
隐式格式:
有界性条件自动满足
C-N 格式:
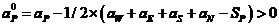
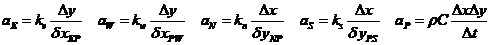
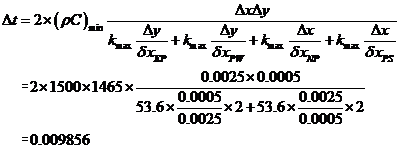
二、控制离散方程:
微分形式的控制方程:
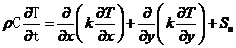
积分形式的控制方程:
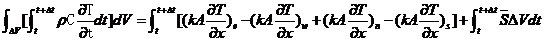
积分可得:
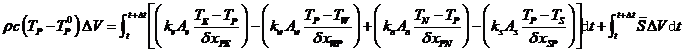
对右式时间积分加权处理:
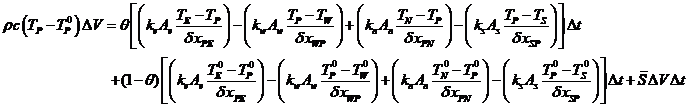
两边同除
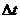
并将面积与体积代入得到:
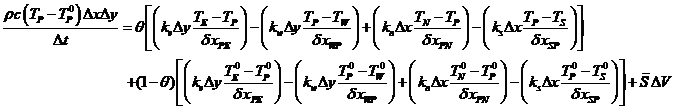
显式形式场变量系数归一化处理:
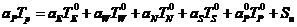
系数:
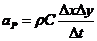
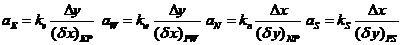
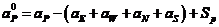
边界条件:
下边界为绝热边界:
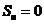
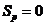

左边界为绝热边界:
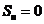
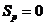
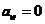
右边界为辐射换热边界:
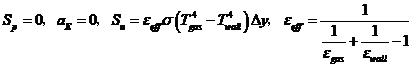
上边界右侧:

上边界左侧:
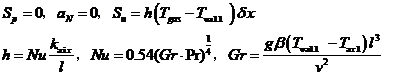
角点的处理:
左上角点:
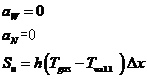
右上角点:
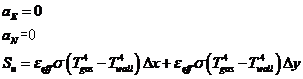
对于 Twall 的处理
左下角点:
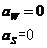
右下角点:
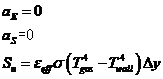
两材料交界面的处理:
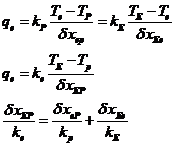
两材料交界面处节点的导热系数
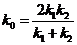
三、编程计算(代码见附录)
编程计算结果:
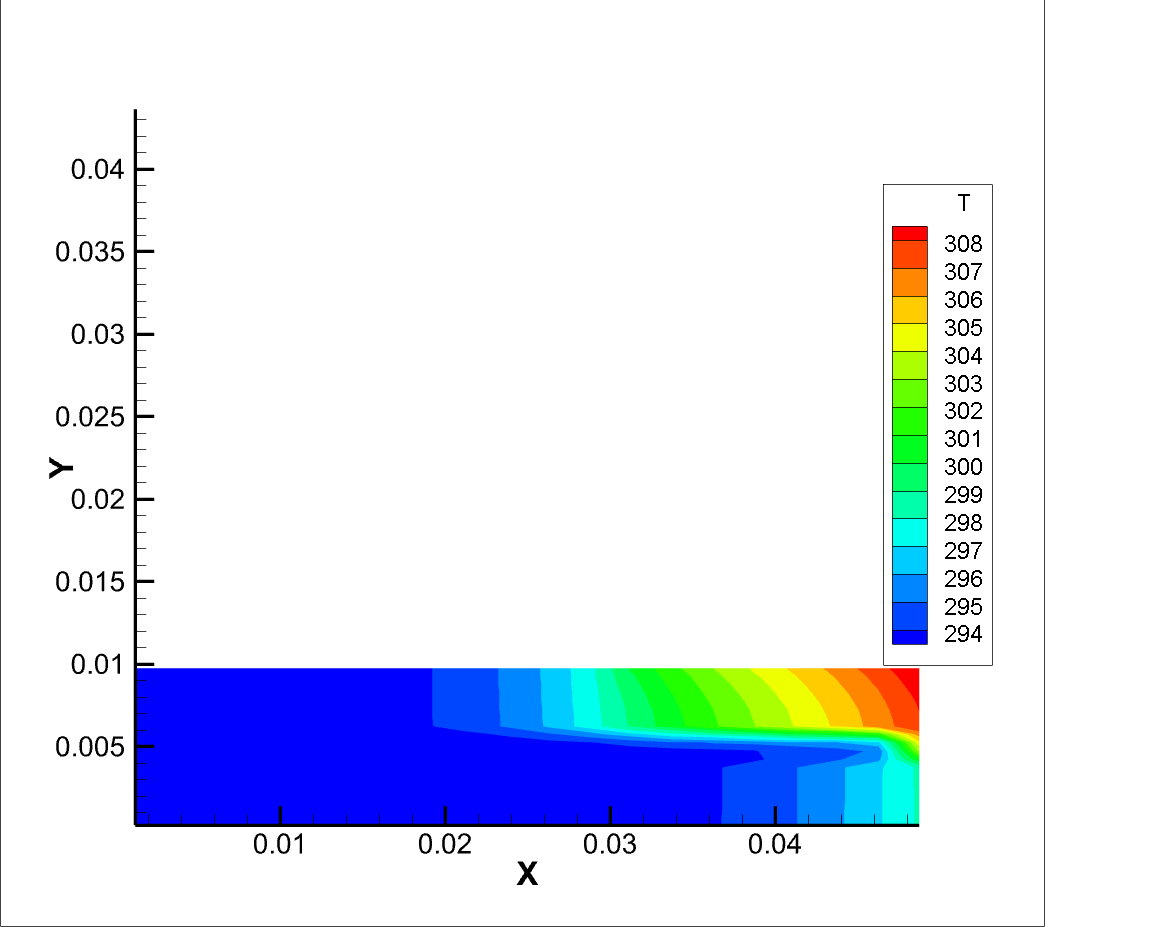
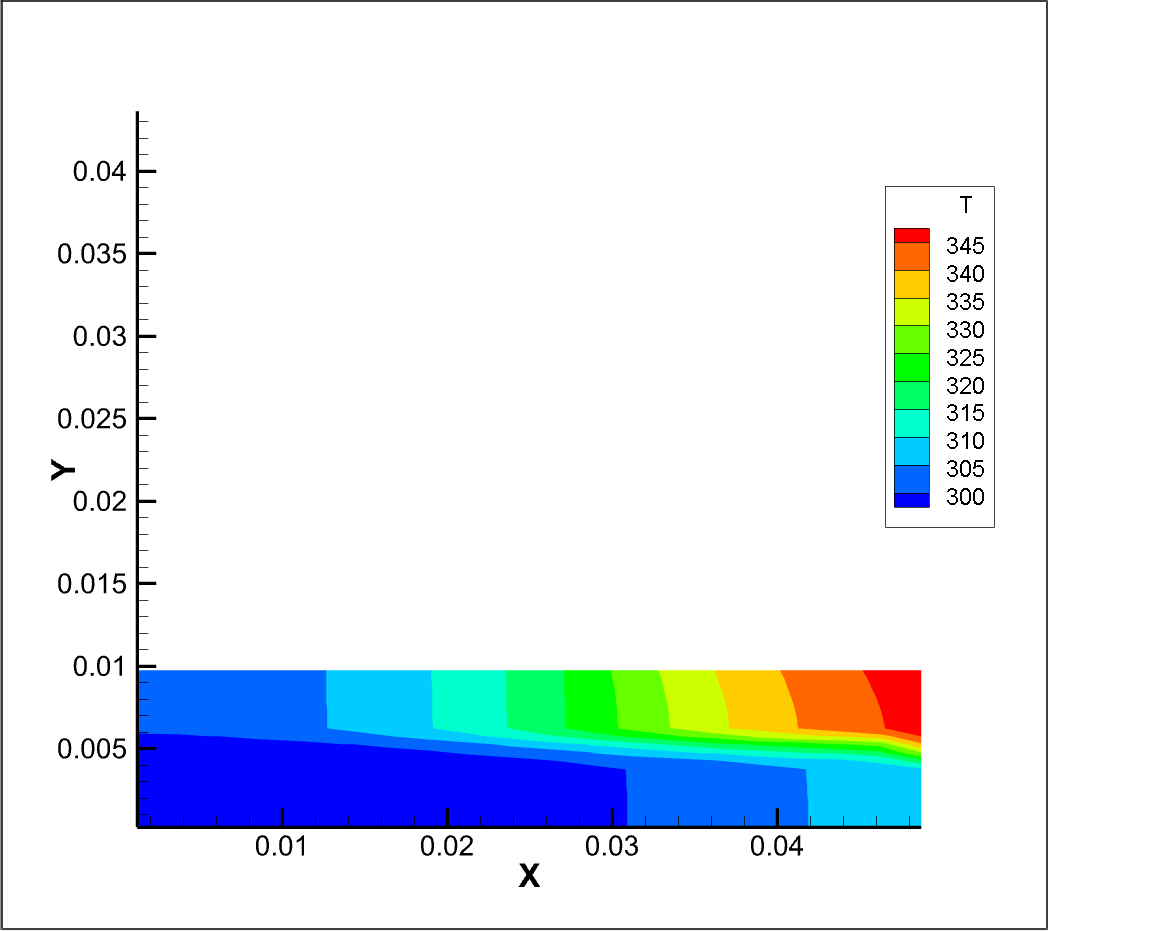
T=5 s 温度分布 T=30 s 温度分布
四、fluent 仿真计算

T=5 s 温度分布

T=30 s 温度分布
五、结论分析
从编程绘制的云图和 fluent 仿真得到的云图都可以看到,由于高温辐射区域在上边的右半部分和右侧区域,所以每一块材料的温度分布都是从右上往左下依次递减的。而温度最高点出现在材料二的右上角而不是材料一的右上角,可能原因是材料一的热传导系数远大于材料二的热传导系数,且材料二的传导系数较小,温度传导速度慢,导致温度最高。
我们还可以看到编程得到的温度比仿真得到的温度低一些,由于边界条件和网格划分均是相同的,所以很有可能是这两种算法在进行迭代时的迭代误差导致的。
六、附录
详细代码
```python
!usr/bin/env python
- - coding:utf-8 _ -
""" @author:tianchang ```
@file: 膏体 14-10.py
```python @time: 2019/11/16 14:10-20s """
添加中断后继续的代码部分
二维非稳态导热问题的有限体积数值解法
from mpl_toolkits.mplot3d import Axes3D from scipy import linalg import matplotlib.pyplot as plt import numpy as np
定义求解函数,形参为网格数目
import os ```
def 打开 tecplot(N_x_grid, N_y_grid, delta_t, eff_1, h, eff_2):
c++
args = 'cd "内流场大作业代码上边界对流eff_1={3} eff_2={5} h={4}"&&"T-2d-Nx={0}-Ny={1}-t={2}.plt"'.format(
N_x_grid, N_y_grid, (int(5 / delta_t)) * 0.004, eff_1, h, eff_2)
os.popen(args)
args = 'cd "内流场大作业代码上边界对流eff_1={3} eff_2={5} h={4}"&&"T-2d-Nx={0}-Ny={1}-t={2}.plt"'.format(
N_x_grid, N_y_grid, (int(30 / delta_t)) * 0.004, eff_1, h, eff_2)
os.popen(args)
def 数据写入文件(
```c++
eff_1,
eff_2,
h,
N_x_grid,
N_y_grid,
k,
X,
Y,
T,
a_p,
a_n,
a_s,
a_w,
a_e,
sp,
su):
'''# 判断是否存在文件夹,不存在则建立'''
if not os.path.exists(
r'./内流场大作业代码上边界对流eff_1={0} eff_2={2} h={1}'.format(eff_1, h, eff_2)):
os.mkdir(
r'./内流场大作业代码上边界对流eff_1={0} eff_2={2} h={1}'.format(eff_1, h, eff_2))
with open(
r'./内流场大作业代码上边界对流eff_1={3} eff_2={5} h={4}/T-2d-Nx={0}-Ny={1}-t={2}.plt'.format(
N_x_grid, N_y_grid, (k + 1) * 0.004, eff_1, h, eff_2), 'w', encoding='UTF-8') as fp1:
fp1.write("VARIABLES = X, Y, T, ap,an,as,aw,ae,sp,su\n") # 按计算节点数输出结果
fp1.write("ZONE I=%d,J=%d, F=POINT,t=\"%.3f\"\n" %
_x_grid, N_y_grid, (k + 1) * 0.004))
for j in range(N_y_grid - 1, -1, -1):
for i in range(0, N_x_grid):
fp1.write(
"{:.5f} {:.5f} {:.3f} {:.3f} {:.3f} {:.3f} {:.3f} {:.3f} {:.3f} {:.3f}\n".format(
,
,
,
a_p[i][j],
a_n[i][j],
a_s[i][j],
a_w[i][j],
a_e[i][j],
sp[i][j],
su[i][j]))
def solve(N_x_grid, N_y_grid, t, eff_1, eff_2, h):
'''N_x_grid, N_y_grid, t, eff, h'''
物性参数定义:发动机长度,高温辐射区域长度,两层材料的宽度、热传导系数、密度、比热容,燃气温度,发射率,对流换热系数
= 0.05
= 0.02
HH = 0.004
hh = 0.002
= 53.6
= 0.2093
= 0.41697
rou1 = 7830
rou2 = 1500
Cp1 = 465
Cp2 = 1465
Tair = 293
Tgas = 923
= 293 # 初始温度
eff = 0.8 # 假定发射率
h = 10 # 假定导热系数
sigma = 5.67 * 10 ** -8
网格尺寸定义: delta_x = L / N_x_grid # 0.0025
delta_y = (2 * HH + hh) / N_y_grid # 0.0005
时间步长及迭代次数: delta_t = 0.004
cal_num = int(t / delta_t)
定义求解线性方程组的动态数组:
AA = np.zeros((N_x_grid * N_y_grid, N_x_grid * N_y_grid))
print(AA)
CC = np.zeros((N_x_grid * N_y_grid))
定义初始0矩阵:
a_w = np.zeros((N_x_grid, N_y_grid))
a_e = np.zeros((N_x_grid, N_y_grid))
a_n = np.zeros((N_x_grid, N_y_grid))
a_s = np.zeros((N_x_grid, N_y_grid))
sp = np.zeros((N_x_grid, N_y_grid))
su = np.zeros((N_x_grid, N_y_grid))
a_p = np.zeros((N_x_grid, N_y_grid))
a_p0 = np.zeros((N_x_grid, N_y_grid))
= np.zeros((N_x_grid, N_y_grid))
X = np.zeros((N_x_grid, N_y_grid))
= np.zeros((N_x_grid, N_y_grid))
离散方程系数计算
for k in range(0, cal_num):
if k == 0:
for i in range(0, N_x_grid):
for j in range(0, N_y_grid):
= T0
for i in range(0, N_x_grid):
for j in range(0, N_y_grid):
结点位置确定
= delta_y * (j + 0.5)
= delta_x * (i + 0.5)
给定初始温度场
判断结点在哪一区域,给出a_e,a_w,a_s,a_n,a_p相应系数
if j <= 0.4 * N_y_grid - 1 or j >= 0.6 * N_y_grid:
0——7,12——19
a_w[i][j] = k1 / delta_x * delta_y # 10.72
a_e[i][j] = k1 / delta_x * delta_y # 10.72
a_s[i][j] = k1 / delta_y * delta_x # 268
a_n[i][j] = k1 / delta_y * delta_x # 268
a_p[i][j] = rou1 * Cp1 * delta_x * delta_y / delta_t
else:
8——11
a_w[i][j] = k2 / delta_x * delta_y
a_e[i][j] = k2 / delta_x * delta_y
a_s[i][j] = k2 / delta_y * delta_x
a_n[i][j] = k2 / delta_y * delta_x
a_p[i][j] = rou2 * Cp2 * delta_x * delta_y / delta_t
交界面处系数
if j == 0.6 * N_y_grid - 1 or j == 0.4 * N_y_grid - 1:
7,11
a_n[i][j] = k0 / delta_y * delta_x
if j == 0.6 * N_y_grid or j == 0.4 * N_y_grid:
8,12
a_s[i][j] = k0 / delta_y * delta_x
边界条件
if i == 0:
左边界为绝热边界
a_w[i][j] = 0.0
su[i][j] = 0.0
sp[i][j] = 0.0
if i == N_x_grid - 1:
右边界为辐射换热边界
if j <= 0.4 * N_y_grid - 1 or j >= 0.6 * N_y_grid:
0——7,12——19
a_e[i][j] = 0.0
将边界结点的温度作为壁面温度
su[i][j] = eff_1 * sigma * \
(Tgas ** 4 - (T[i][j]) ** 4) * delta_y
sp[i][j] = 0.0
else:
a_e[i][j] = 0.0
将边界结点的温度作为壁面温度
su[i][j] = eff_2 * sigma * \
(Tgas ** 4 - (T[i][j]) ** 4) * delta_y
sp[i][j] = 0.0
if j == 0:
下边界为绝热边界
a_s[i][j] = 0.0
su[i][j] = 0.0
sp[i][j] = 0.0
if j == N_y_grid - 1:
上边界为混合边界
if i <= N_x_grid * 0.6 - 1:
上边界左侧为对流换热
a_n[i][j] = 0.0
su[i][j] = h * (Tair - T[i][j]) * delta_x
sp[i][j] = 0
else:
改动1: 上边界右侧为辐射换热加对流换热
a_n[i][j] = 0.0
su[i][j] = eff_1 * sigma * \
(Tgas ** 4 - (T[i][j]) ** 4) * delta_x + h * (Tair - T[i][j]) * delta_x
sp[i][j] = 0.0
四个角点系数替换
if i == 0 and j == 0:
左下角点
su[i][j] = 0.0
if i == 0 and j == N_y_grid - 1:
左上角点
su[i][j] = h * (Tair - T[i][j]) * delta_x
if i == N_x_grid - 1 and j == N_y_grid - 1:
右上角点
su[i][j] = eff_1 * sigma * (Tgas ** 4 - (T[i][j]) ** 4) * delta_x + eff_1 * sigma * (
Tgas ** 4 - (T[i][j]) ** 4) * delta_y + h * (Tair - T[i][j]) * delta_x
if i == N_x_grid - 1 and j == 0:
右下角点
su[i][j] = eff_1 * sigma * \
(Tgas ** 4 - (T[i][j]) ** 4) * delta_y
a_p0[i][j] = a_p[i][j] - \
_w[i][j] + a_e[i][j] + a_s[i][j] + a_n[i][j] - sp[i][j])
将系数给入系数矩阵AA,CC
for i in range(0, N_x_grid):
for j in range(0, N_y_grid):
AA[i * N_y_grid + j][i * N_y_grid + j] = a_p[i][j]
CC[i * N_y_grid + j] = su[i][j] + a_p0[i][j] * T[i][j]
if j != 0:
CC[i * N_y_grid + j] = CC[i * N_y_grid + j] + \
a_s[i][j] * T[i][j - 1]
if j != N_y_grid - 1:
CC[i * N_y_grid + j] = CC[i * N_y_grid + j] + \
a_n[i][j] * T[i][j + 1]
if i != 0:
CC[i * N_y_grid + j] = CC[i * N_y_grid + j] + \
a_w[i][j] * T[i - 1][j]
if i != N_x_grid - 1:
CC[i * N_y_grid + j] = CC[i * N_y_grid + j] + \
a_e[i][j] * T[i + 1][j]
result = linalg.solve(AA, CC) # 求解温度场
```
T_对流求和 = 0
T_对流求和_i = 0
```python for i in range(0, N_x_grid): for j in range(0, N_y_grid): = result[i * N_y_grid + j] if j == N_y_grid - 1:
上边界为混合边界
if i <= N_x_grid * 0.6 - 1:
上边界左侧为对流换热
```
T_对流求和 += T[i][j]
T_对流求和_i += 1
```c++
print (T_对流求和, T_对流求和_i)
```
delta_t_温差 = T_对流求和 / T_对流求和_i - 293
数据写入文件(eff_1, eff_2,h,N_x_grid,N_y_grid,k,X,Y,T,a_p,a_n,a_s,a_w,a_e,sp, su)
c++
print('已完成:{:.2f}% t_温差:{:.3f}'.format(k / cal_num * 100, delta_t_温差))
打开 tecplot(N_x_grid, N_y_grid, delta_t, eff_1, h, eff_2) # 最后调用
```python
return (X, Y, T)'''
调用函数的主程序
solve(20, 20, 30, 0.8, 0.3, 0.3) # eff_1=0.3,h=10 ```
参考文献
- 锦化氯碱车间信息管理系统设计(吉林大学·岳长海)
- 基于J2EE的Web应用研究(河海大学·朱春江)
- 基于J2EE平台的Web应用系统研究(武汉理工大学·马黎明)
- 柴油机拆装多媒体CAI课件设计与开发(大连理工大学·杨定国)
- 用统一过程构建J2EE企业应用(天津大学·巩兰杰)
- 相变存储材料基因数据库的设计和应用(华中科技大学·于闰)
- 基于.NET的动态信息发布系统的设计与实现(重庆大学·胡轶众)
- 电驱动整车动力学仿真软件平台搭建与开发(湖南大学·黄明耀)
- 柴油机拆装多媒体CAI课件设计与开发(大连理工大学·杨定国)
- 民航发动机健康管理数据库设计与故障诊断(中国民航大学·张煜)
- 用统一过程构建J2EE企业应用(天津大学·巩兰杰)
- 发电过程中供热机组调峰特性在线监测系统(吉林大学·吴轶夫)
- 发动机设计参数正向开发平台建设及应用(湖南大学·徐新生)
- 基于J2EE的远程网络教育系统研究与实现(电子科技大学·陈南荪)
- 基于J2EE和MVC模式的Web应用研究(武汉理工大学·刘继华)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕设助手 ,原文地址:https://bishedaima.com/yuanma/35882.html











