多项式拟合正弦函数
一、实验过程
实验目的
掌握最小二乘法求解(无惩罚项的损失函数)、掌握加惩罚项(2 范数)的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)
实验要求
生成数据,加入噪声;
用高阶多项式函数拟合曲线;
用解析解求解两种 loss 的最优解(无正则项和有正则项);
优化方法求解最优解(梯度下降,共轭梯度);
用你得到的实验数据,解释过拟合。
用不同数据量,不同超参数,不同的多项式阶数,比较实验效果。
语言不限,可以用 matlab,python。求解解析解时可以利用现成的矩阵求逆。梯度下降,共轭梯度要求自己求梯度,迭代优化自己写。不许用现成的平台,例如 pytorch,tensorflow 的自动微分工具。
实验环境
OS: Windows 11
Python: 3.7.9
设计思想
生成数据并加入噪声

利用高阶多项式函数拟合曲线(无正则项)
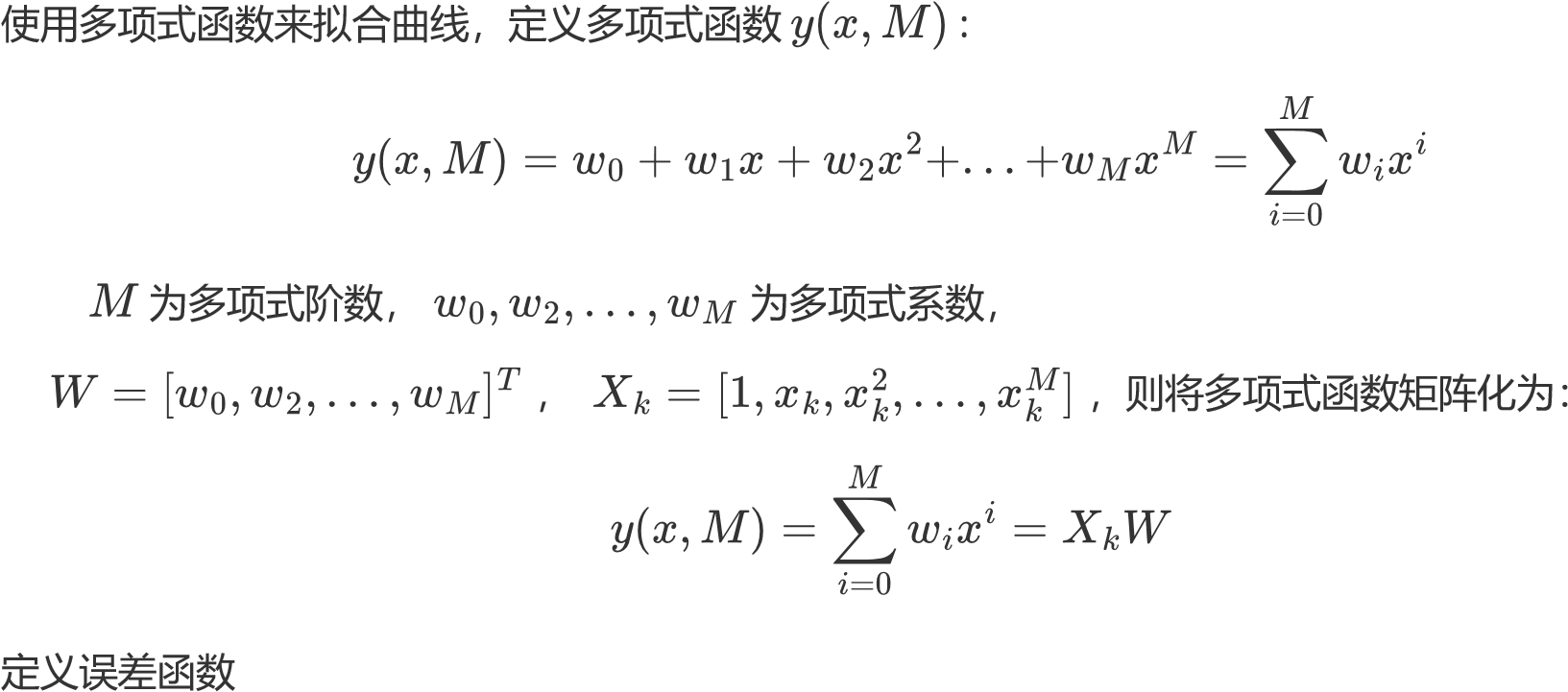

代入 即可得到 获得拟合曲线。
利用高阶多项式函数拟合曲线(有正则项)
通过正则化减轻过拟合影响,为误差函数增加一个惩罚项如下:

代入
梯度下降法求解最优解
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向;对应的,梯度的反方向就是给定点的下降最快的方向。梯度下降公式为 ,其中 为学习率或步长对有惩罚项的误差函数:
共轭梯度法求解最优解
考虑线性对称正定方程组: 构造二次函数:
对其求导得:
则求 的解即为求函数
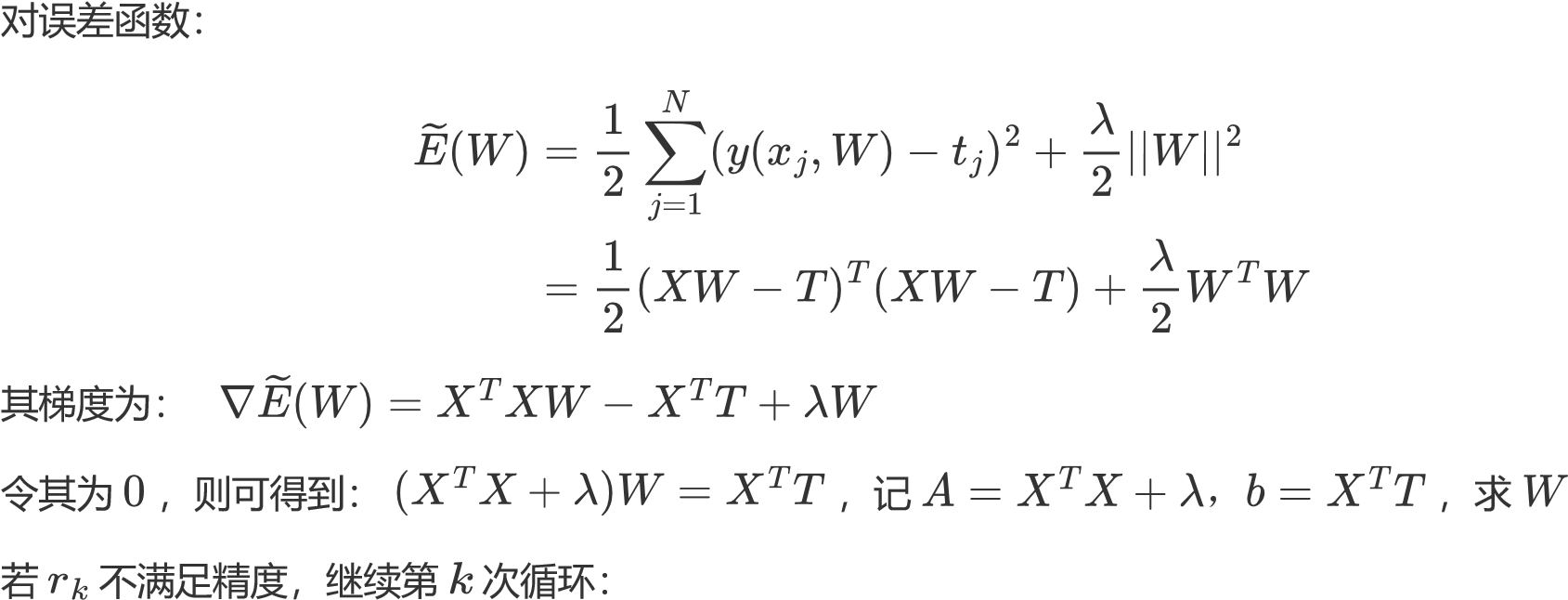
直到满足精度,退出循环,得到
二、实验结果分析
不带正则项的解析解

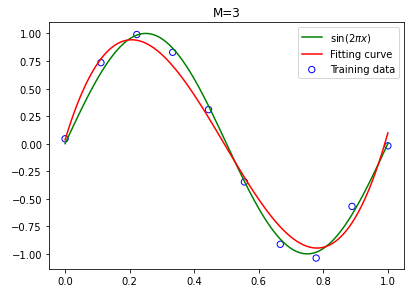

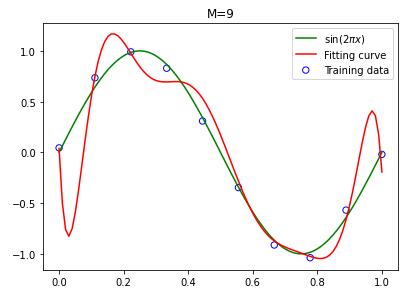
- 在 1 阶时,无法拟合,属于欠拟合,需要提高阶数;
- 在 3 阶时,拟合效果较好,阶数提高到 5 阶,拟合效果更好;
- 阶数提高到 9 阶,拟合函数图像能穿过大多数训练集上的点,但波动较大,出现过拟合现象。
可以通过增加训练集大小降低过拟合的影响:
设定阶数为 9 阶,在训练集大小分别为 10,20,50,100 下拟合结果:
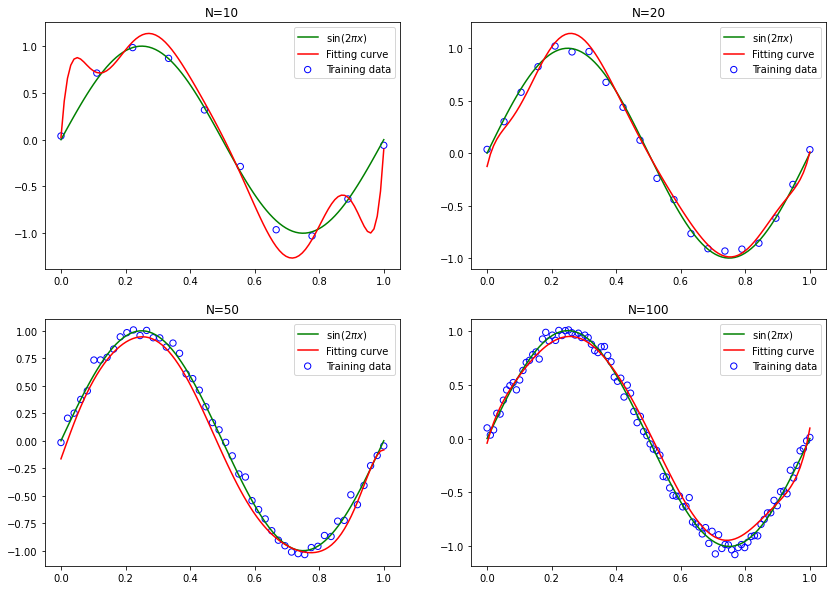
随着训练集增大,过拟合现象逐渐消失,拟合函数很好的拟合到原函数上。
带正则项的解析解 取训练集大小为 10,验证集大小为 20,阶数为 9,确定最优

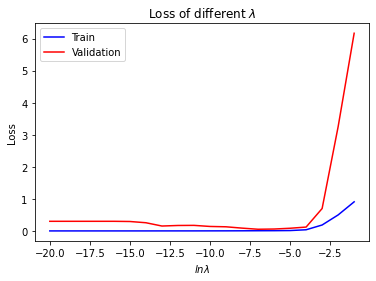
取 为 ,在训练集大小为 10 ,阶数为 9 的条件下的带惩罚项和不带惩罚项的拟合图像比较

可以看出,加入惩罚项有效降低过拟合现象。
梯度下降求得优化解
设定 为 ,学习率 为 0.01,(左图精度为 ,右图精度为 )设定训练集大小为 10 ,在不同阶数下拟合函数:
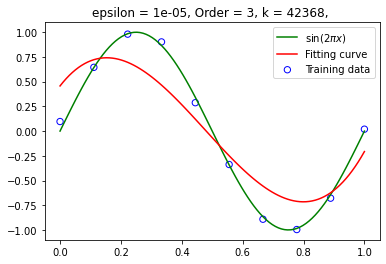

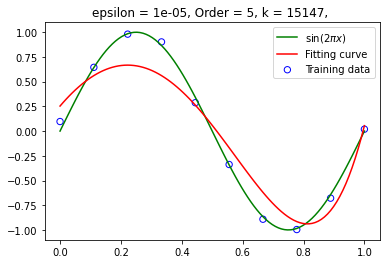
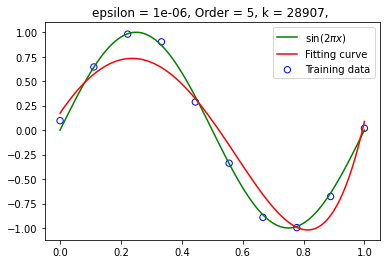

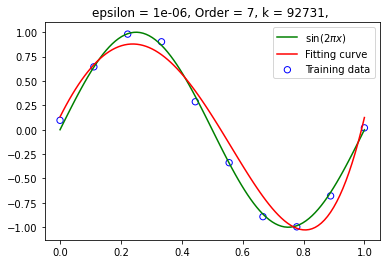
阶数为 9:
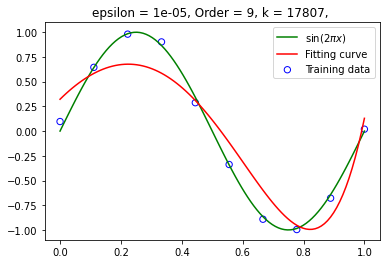

设定阶数为 9,在不同训练集大小下拟合函数 训练集大小为 20:
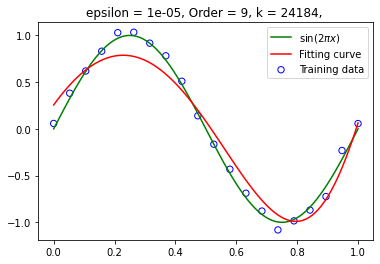
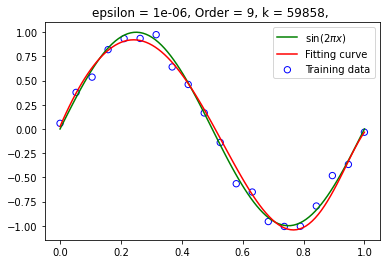
训练集大小为 50:
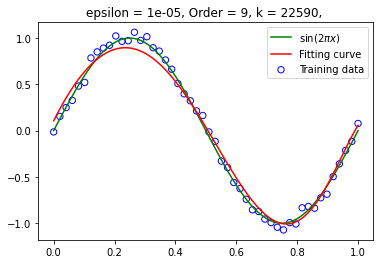
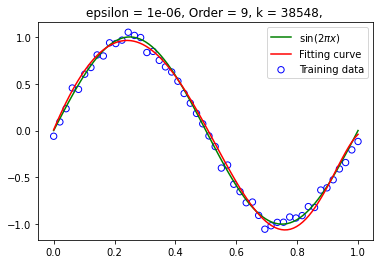
精度升高,迭代次数变大;多项式阶增大,迭代次数呈现下降趋势;而训练集的大小对于迭代次数几乎没有影响,但仍然满足训练集越大拟合效果也好的结论。
共轭梯度求得优化解
设定 为 ,(左图精度为 ,右图精度为 )设定训练集大小为 10 ,在不同阶数下拟合函数: 阶数为 3 :
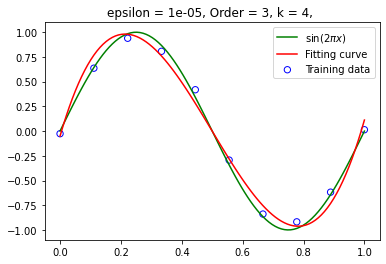



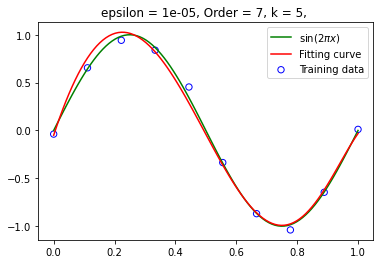
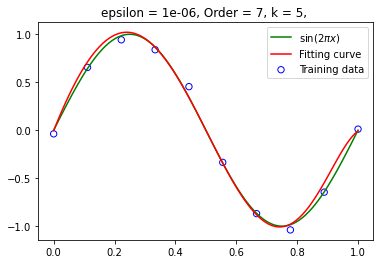
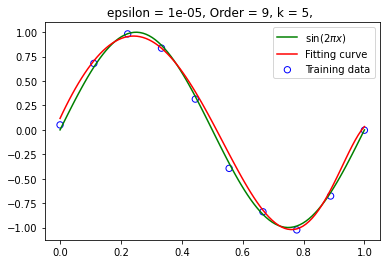

设定阶数为 9,在不同训练集大小下拟合函数 训练集大小为 20:
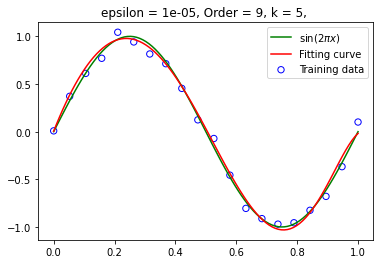
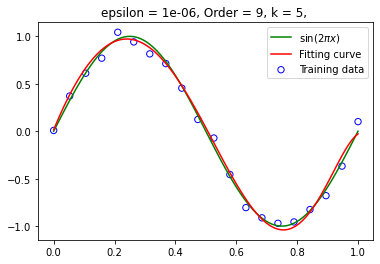
训练集大小为 50:
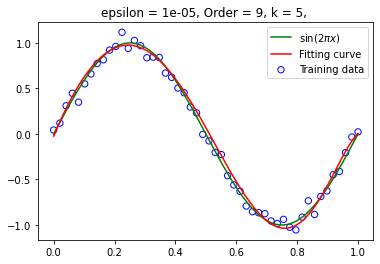
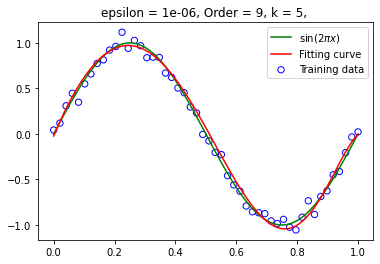
的右图的拟合效果并未显著强于精度为 下的拟合效果。
共轭梯度法的迭代次数受精度、多项式阶、训练集的大小的影响并不大,一直在
三、结论
在对正弦函数的多项式拟合中,不加惩罚项时,多项式的次数越高,拟合得越好,阶数较高时出现过拟合现象,是由于样本数量少但模型能力强,模型拟合结果过分依赖数据集,这种强拟合能力可能无法拟合出正弦曲线的效果。所以增大数据集可以有效地解决过拟合问题。
加入惩罚项后,过拟合现象得到改善。加入惩罚项可以有效地降低参数的绝对值,从而使模型复杂度与问题匹配。所以对于训练样本限制较多的问题,增加惩罚项是解决过拟合问题的有效手段。
在使用梯度下降时,由于我们的目标函数是二次的,只有一个极值点,即最值点,所以梯度下降的初值选取并不很重要。如果梯度下降步长设置的比较大,那么下降结果将在目标函数最值附近逐渐向上跳动,从而无法收敛。
梯度下降相比共轭梯度收敛速度很慢,迭代次数很大,而共轭梯度的稳定性较差,更容易出现过拟合现象,但对于数据量较大复杂度较高的情况,共轭梯度显然要比梯度下降来的更优。
四、参考文献
《模式识别与机器学习》
《机器学习》
参考文献
- 基于.NET的在线考试系统的设计与实现(吉林大学·杨雪洁)
- 偏微分方程有限差分法求解软件研发(宁夏大学·马天龙)
- 多维数据展现开发工具的设计与实现(山东大学·展鹏)
- 基于B/S的考卷搜索和标记系统的设计与实现(华中师范大学·沈亮)
- 多维数据展现开发工具的设计与实现(山东大学·展鹏)
- 基于J2EE网络考试系统的设计与实现(吉林大学·叶丽娜)
- 基于SSH框架的软件项目管理系统的设计与实现(北京邮电大学·王萌)
- 基于Web的负荷统计法建模平台(山东大学·刘晓宇)
- 基于行列转换的统计功能研究与应用(中国海洋大学·张娜)
- 双权重弹性网-逻辑回归多步筛选算法及其应用(中央财经大学·黄捷)
- 基于Q-learning的系统集成与过程优化(青岛科技大学·魏晓彤)
- 中学python课程知识图谱构建及应用研究(华中师范大学·黄健)
- 基于Web的微分方程自动求解系统的研究与开发(华东师范大学·杨乐)
- 基于J2EE的远程网络教育系统研究与实现(电子科技大学·陈南荪)
- 基于Java和Matlab的虚拟仿真实验系统的设计与实现(长江大学·喻盼)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕设驿站 ,原文地址:https://bishedaima.com/yuanma/36164.html











