无缝图像拼接
运行说明
首先安装依赖的第三方库:
c++
sudo apt install cmake libcgal-dev libcgal-qt5-dev
sudo pip2 install opencv-python
然后编译 C++ 文件:
c++
cmake .
make
在当前目录下生成可执行文件 main。
使用命令
c++
./main <args>
即可运行或查看帮助,如图 1 所示:
图 1: 查看帮助
实现方式
考虑到实现效率,我采用 C++ 编写代码,其中图片的读入和输出采用 GitHub 上的开源仓库"stb"实现,图片边缘的提取采用 OpenCV。
算法细节
MVC
MVC[3, 2] 算法可分为如下步骤:
找出所有的边缘像素点的位置;
使用 CGAL 将这些点进行带约束的三角剖分;
对于三角剖分结果中的非边缘像素点,依据论文中给出的权重计算方式算出这个点所要垫高的权值;
对于每个三角面片,已经求出了三个顶点的垫高的权值,并且由于假设函数在该范围内平滑,因此直接用一个平面去拟合三角形内的所有像素点的权值大小即可。
图 2 展示了 MVC 算法的中间结果,图 2(a)显示的是从 mask 中找到边缘之后的可视化效果,图 2(b)显示的是从这些边界上的点生成三角剖分的网格之后的效果。请注意,原图并不是一个凸多边形,因此在三角剖分之后要手动去掉那些不在轮廓内的三角形,具体可以采用射线法判断某个点是否在多边形内的算法即可。

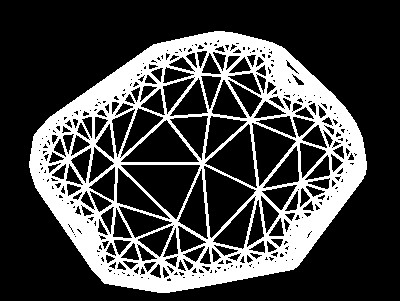
边界分割 (b) 三角剖分结果图 2: MVC 可视化中间步骤
1.2 Poisson
此外我还实现了泊松图像融合算法 [4, 5] 进行对比,其梯度计算方式为
(x,y) = 4I(x,y) I(x 1,y) I(x,y 1) I(x +1,y) I(x,y +1)
将原图求完梯度之后,将该梯度匹配到目标图上的某一区域,本质上是一个解线性方程组的问题。形式化地,设有 N 个像素点需要匹配到目标图片中,则需要求解线性方程组Ax =b
其中 x 代表融合后的图片中像素点的值,矩阵 A 的大小 N ×N,列向量 x 和 b 的大小 N,并且 A 的每一行至多只有 5 个非零元素,并且对角线上的元素均为 4。
是一个巨大的稀疏矩阵。考虑到矩阵求逆的复杂度为 O(N3) 太高,并且某些情况下连都无法直接以矩阵形式存储,因此无法直接从公式
x = A1b
求得 x。此处采用 Jacobi Method 迭代求解出 x 的值,详见 [1]。
1.3 实验结果
1.3.1 Test1
使用命令
c++
time ./main -s img/src3.jpg -t img/target1.jpg -m img/mask3.jpg -o result_MVC.png -h -135 -w -30 -a MVC
time ./main -s img/src3.jpg -t img/target1.jpg -m img/mask3.jpg -o result_Poisson.png -i 5000 -h 50 -w 100 -a Poisson
可得到如下结果
```c++ Done with 262 vertices and 466 triangles. real 0m0.243s user 0m0.287s sys 0m0.233s
iter 5001
err 0.001767 0.001913 0.003486
real 0m0.361s
user 0m0.345s
sys 0m0.016s
```
可以看到,MVC 总共只用了 262 个三角顶点,耗时 0.243s;Poisson 由于使用迭代方法求解矩阵,迭代次数越多解的越精确,5000 轮之后误差几乎为 0,并且运行速度为 0.36s,二者均十分快。合成效果如图 3 所示。由于该样本太容易合成,二者在效果上看不出有什么明显差别。

图 3: 第一组数据合成效果
1.3.2 Test2
使用命令
c++
time ./main -s img/src4.png -t img/target2.png -m img/mask4.png -o result_MVC.png -h 142 -w 132 -a MVC
time ./main -s img/src4.png -t img/target2.png -m img/mask4.png -o result_Poisson.png -i 10000 -h 150 -w 150 -a Poisson
可得到如下结果
```c++ Done with 836 vertices and 1580 triangles. real 0m0.233s user 0m0.228s sys 0m0.305s
iter 10001
err 82.519269 49.665685 58.341544
real 0m5.356s
user 0m5.351s
sys 0m0.004s
```
可以看到 MVC 总共只用了 836 个三角顶点,耗时 0.228s;Poisson 在 10000 轮之后总误差不到 100,平均每个像素点误差不到 0.01,并且运行速度为 5s 左右。合成效果如图 4 所示,对比可以发现 MVC 的边缘比 Poisson 更加平滑。


MVC (b) Poisson 图 4: 第二组数据合成效果
1.3.3 Test3
使用命令
c++
time ./main -s img/src0.jpg -t img/target0.jpg -m img/mask0.png -h
318 -w 370 -o result_MVC.png
time ./main -a Poisson -s img/src0.jpg -t img/target0.jpg -m img/ mask0.png -o result_poisson.png -i 10000 -h 350 -w 400
可得到如下结果
```c++ Done with 1702 vertices and 3346 triangles. real 0m0.420s user 0m0.458s sys 0m0.253s
iter 10001
err 2238.275301 1683.477450 1885.838338
real 0m43.901s
user 0m43.816s
sys 0m0.040s
```
这是 MVC 论文中的图,可以看到 MVC 总共只用了 1702 个三角顶点,耗时 0.458s;
Poisson 在 10000 轮之后总误差大约 2000,平均每个像素点误差不到 0.03,但是运行速度达到了 43s 左右。合成效果如图 5 所示。从效果上看而言还是 MVC 更胜一筹。


MVC (b) Poisson 图 5: 第三组数据合成效果
c++
References
Jacobi method. . Accessed: 2018-04-12.
Kewei Chen and Chenen Wu. Mvc. . Accessed: 2018-06-12.
Zeev Farbman, Gil Hoffer, Yaron Lipman, Daniel Cohen-Or, and Dani Lischinski. Coordinates for instant image cloning. ACM Transactions on Graphics (TOG), 28(3):67, 2009.
Patrick Pérez, Michel Gangnet, and Andrew Blake. Poisson image editing. ACM Transactions on graphics (TOG), 22(3):313--318, 2003.
Christopher J. Tralie. Poisson image editing. Accessed: 2018-04-12.
参考文献
- 印刷公司内容管理平台的设计与实现(吉林大学·郎彩虹)
- 智能服装款式设计系统的数据库实现和远程数据获取(东华大学·万登峰)
- 基于Java Web的牧草种子显微图像拼接系统的研究与实现(内蒙古农业大学·宁丽娜)
- 家居导购数据平台的设计与实现(北京交通大学·李昊)
- 建筑设计院图档管理系统的设计与实现(吉林大学·时淮龙)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于B/S架构的工程图纸管理系统(辽宁科技大学·孔庆涛)
- 基于DNN生成商品外观设计图的Web应用的设计与实现(大连海事大学·杨书雯)
- 基于DNN生成商品外观设计图的Web应用的设计与实现(大连海事大学·杨书雯)
- 基于PHP+MySQL的交互学习系统的设计与实现(吉林大学·刘博)
- 基于.NET自定义控件的社区网站系统研究与实现(武汉理工大学·刘亚)
- 基于J2EE的手机综合网站的设计与实现(吉林大学·宋微)
- 基于B/S架构的工程图纸管理系统(辽宁科技大学·孔庆涛)
- Linux环境下基于Web的图档管理系统的开发(山东科技大学·刘治国)
- 家居导购数据平台的设计与实现(北京交通大学·李昊)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕设驿站 ,原文地址:https://bishedaima.com/yuanma/36040.html











