迷宫求解
一、必做任务一
使用强化学习算法,对于给定的迷宫,训练老鼠在迷宫中寻找蛋糕。

迷宫与图中类似,黑色格子为墙,不能走,老鼠试图走向墙时,会停在原地。白色格子为空地,可以走。黄色圆圈标志老鼠走过的格子,五角星为老鼠所在位置。起始位置为左上角,结束位置为右下角。
二、必做任务二
自行生成不同迷宫(尺寸、地图),完成前述操作。
我对这个任务的理解是:程序中事先定义好了一些不同大小和样式的迷宫,供用户挑选,此外,用户也可以自己定义迷宫。
三、必做任务三
若迷宫中存在老鼠夹子,且位置固定,完成前述操作。
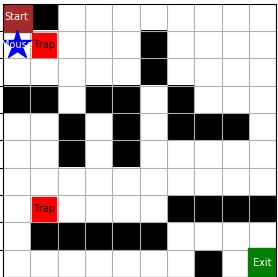
如图,红色方格代表陷阱,即老鼠夹子。与黑色方格的墙不同,老鼠可以走向陷阱,而一旦走入陷阱,游戏失败。
四、选做任务一
考虑时变因素,如迷宫的某些格子会周期性产生火焰。

如图,红色三角为火焰,和陷阱相同,老鼠可以走向火焰,但一旦走入就会导致游戏失败。
设老鼠每走一步的时间为一个时间单位,火焰在一个周期时间(偶数个时间单位)内的后半段出现,前半段不出现。比如火焰周期为 4,老鼠走两步,火焰出现,再走两步,火焰消失。火焰周期可在用户自定义界面由用户定义。
五、问题建模
5.1 迷宫
迷宫用一个二维数组建模,数组中的每个数代表一个方格,数字值代表方格类型(如 0 表示墙, 2 表示陷阱, 3 表示火)。
迷宫是强化学习中的“环境”,老鼠在迷宫中每走一步(采取一个动作),迷宫会返回一个 reward,游戏状态(输或赢),以及老鼠下一个位置。
reward 基本都是负值,除了到达终点的动作。
| 动作 | Reward |
|---|---|
| 移动 | -0.05 |
| 撞墙 | -0.85 |
| 重复走过的格子 | -0.3 |
| 死亡(陷阱或火焰) | -2 |
| 到达终点 | 1 |
之所以将移动的 reward 设为负值,是为了减少老鼠的路线长度,尽快到达终点。
为防止游戏无止境地进行下去,当 reward 积累到足够小时,游戏也会结束。
5.2 表模型
使用 Q-learning 算法进行训练,就是要得到 Q 表:行动价值函数,对每一个状态的每个动作都有一个行动价值与其对应,做决策时选择当前状态下行动价值最高的动作。
动作:向上下左右四个方向前进。
状态:老鼠所在的格子(引入时间因素后还有考虑时间)。
下图是可视化的 Q 表,从每个状态的四个动作中选出 Q 值最大的一个,用箭头画出来,颜色表示 Q 值大小,从红到绿 Q 值越来越大。
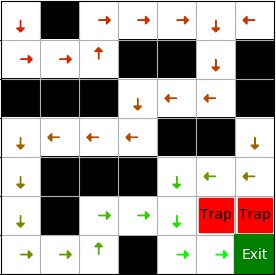
5.3 监督学习模型
除 Q 表模型外,我们也尝试了使用监督学习模型进行预测,将 1 中提到的代表迷宫的二维数组变成一维向量,输入到全连接网络中,网络输出 1 × 4 大小的向量,分别表示四个动作的 Q 值。
使用监督学习模型进行训练时,需要使用批量式价值近似方法。把训练数据存到一个库里,训练时从库里拿一批数据出来训练,即经验回放。注意库的大小有限,库满时删除旧数据,加入新数据。
5.4 -learning 学习过程
Q-learning 是一种离线策略学习的方法,行为策略采用-贪心策略,有利于进行探索,目标策略采用贪心策略,有利于充分利用学到的经验。
具体学习过程如下,在老鼠处于状态 state 时,首先基于当前 Q 表采用-贪心策略进行预测,选择一个动作,采取该动作,从”环境”中得到反馈:下一状态 +1, 回馈 +1, 游戏状态(输赢)game_status。再采用贪心策略对下一状态 +1 进行预测,得到 Q(+1, +1),使用时序差分方法对 Q 表进行更新:
, ) Q(, ) + [+1 + Q(+1, +1) Q(, )]
在每一局游戏的每一步移动都重复上面的步骤,直到游戏结束,一轮游戏叫做一个 epoch。训练会在足够多 epoch 后,或 Q 表足够完善时停止。
5.5 加入时间因子
选做任务中要求火焰周期性变化,因此我们需要在状态中加入时间维度,Q 表也会发生响应的变化。
迷宫问题符合马尔可夫过程的定义,即当前状态下的决策与之前的步骤无关。加入时间因子后也是如此,当前状态下,即考虑时间和老鼠的位置,进行的决策与过去的步骤无关。因此时间因子不是无限大的,但又因为“环境”的反馈与时间有关,所以需要考虑一个周期内的时间因子即可。比如火焰出现周期为 4,则时间变量的取值范围为 0,1,2,3,变化规律为:0 → 1 → 2 → 3 → 0 → 1 → 2 …
在不加入时间因子时,状态由一个二元组表示(x,y),即老鼠的坐标;加入时间因子后,状态由三元组表示(x,y,t)。Q 表也会扩大规模,比如火焰周期为 4 时,Q 表规模会变为原来的 4 倍。
下图是周期为 2 时 Q 表的可视化结果,每个坐标点有两个 Q 值,分别对应时间 0 和时间 1,时间 t 为 1 时火焰出现。

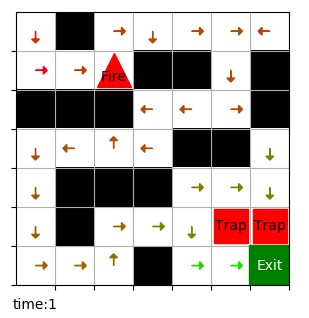
六、算法设计和代码
使用 Q 表模型时,核心算法主要有两个类:迷宫(环境)和 Q 表。我们将 Q 表的存储,
预测,训练等放在一个类中实现。除此之外还有可视化,用户界面等代码中的类。
6.1 迷宫类
- 迷宫信息用一个二维数组表示,数组中的每个数代表一个方格,数字值代表方格类型(如
- 表示墙, 2 表示陷阱, 3 表示火)。
- 迷宫类接收决策动作,给出对应的反馈:下一状态 +1, 回馈 +1, 游戏状态(输赢) game_status。
6.2 表模型类
表类有 Q 值的存储,决策的进行,Q 表的学习等功能函数,进行预测和学习时会与迷宫(“环境”)进行交互,对其输入动作,得到反馈。
七、UI 设计和使用说明
UI 界面使用 pyqt 设计,虽然不方便使用拖放组件的方式设计,但纯编程的设计自由度更高,让我得以实现像用户自定义图形这样的复杂操作。UI 的最高层是一个 QMainWindow 组件,里面有一个标签页,包含三个标签,分别是:“已有迷宫”和“用户自定义”。
7.1 已有迷宫界面
已有迷宫界面允许用户从我们定义好的几个迷宫中选择一个,进行训练并查看完整的走迷宫过程。由于我们已经训练并存储好了这些迷宫的 Q 表,用户也可以不进行训练,直接查看走迷宫过程。
用户可以选择迷宫过程的播放速度,界面左面两个分别是可视化的 Q 表和走迷宫的路线。用户可以从 6 种迷宫中任选其一,6 种迷宫包括 2 种尺寸,3 种类型。3 种类型分别是:只有墙,有墙和陷阱,有火焰。火焰的周期默认为 2.
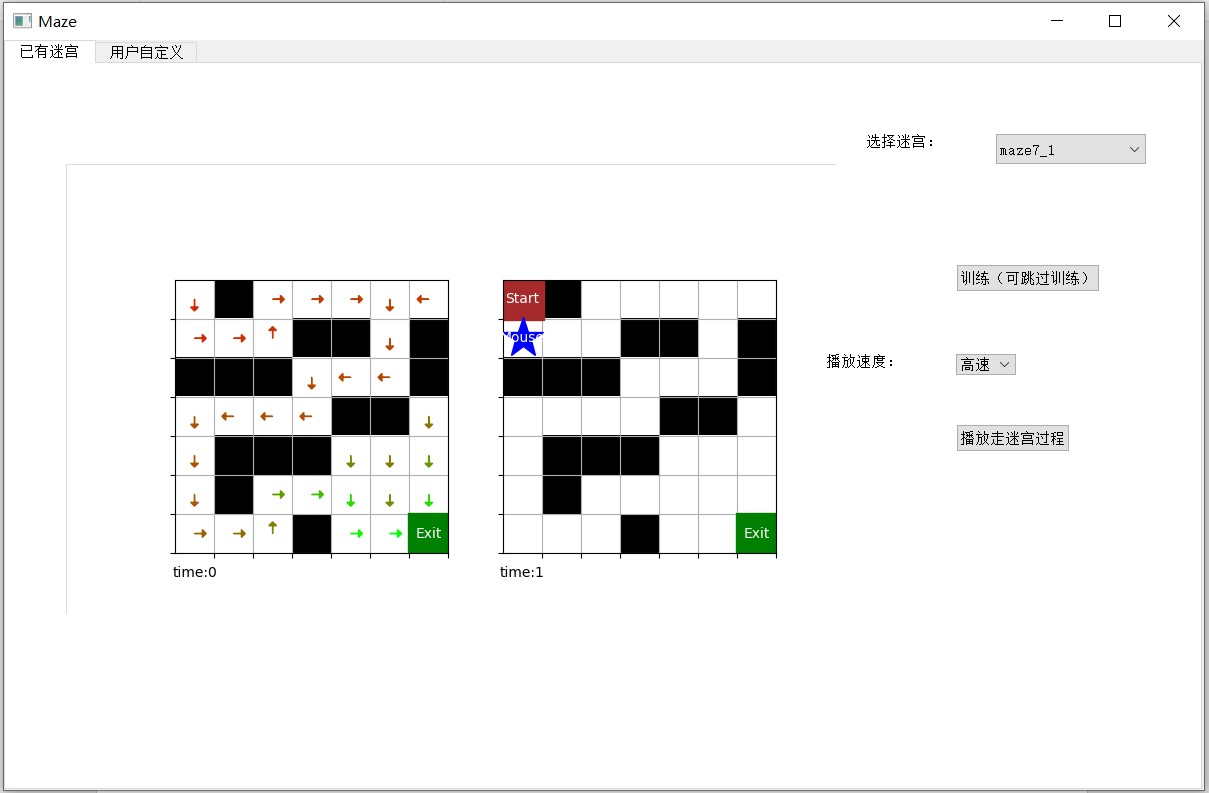
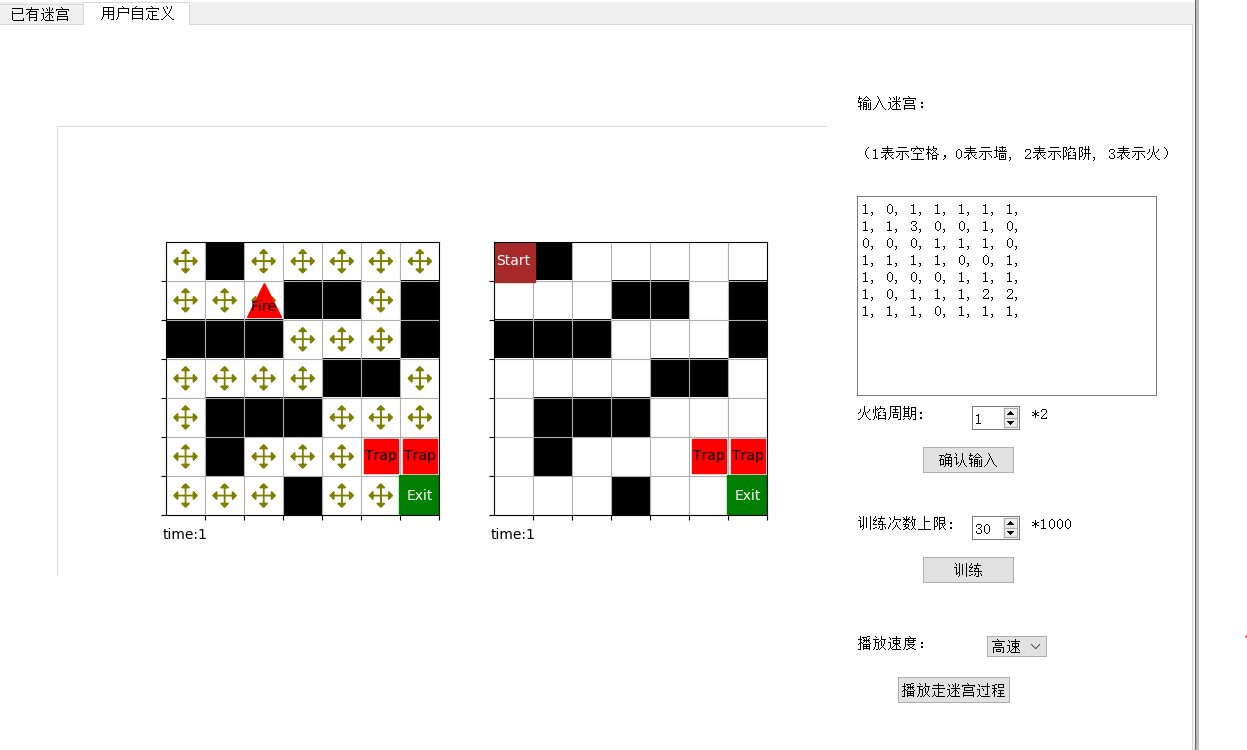
7.2 用户自定义
在用户自定义界面,用户可以输入任意大小的迷宫,自定义火焰周期,训练次数上限。之后进行训练,并以三种不同的速度查看完整的走迷宫结果。下面的 Q 表还没有经过训练,所以所有 4 个方向的 Q 值相等。
八、总结
本次大作业我尝试了 Q 表模型和监督学习模型。
一开始我直观地认为监督学习模型更好,但完成后才发现其训练速度慢,且算法复杂。于是我又实现了 Q 表模型,训练速度很快,且算法直观。这让我体会到分析问题和文献调研的重要性,对不同的问题要用不同的解决方法,从难到易,杀鸡不用宰牛刀。
我完成了三个必做任务和选做任务,并设计了 UI 界面。此外,用户在 UI 界面有很大的自由度,可以自定义迷宫和迷宫参数。
虽然这次大作业花了我较长时间,尝试了两种方案,但体会到了独立完成一个完整项目的乐趣,收获了成就感,不仅提高了我的编程能力,加深了我对强化学习的理解,还提高了我解决问题的能力以及抗压能力,收获满满,也算是付出得到了回报。
参考文献
- 基于Struts架构模式的人才招聘网站开发(大连交通大学·张春国)
- 基于Python的非结构化数据检索系统的设计与实现(南京邮电大学·董海兰)
- 基于.NET平台的游戏门户系统设计与实现(电子科技大学·余胜鹏)
- 基于深度学习的智能问答系统的研究与实现(沈阳师范大学·卓越)
- 基于领域的网络爬虫技术的研究与实现(武汉理工大学·谭龙远)
- 基于.NET自定义控件的社区网站系统研究与实现(武汉理工大学·刘亚)
- 基于网络爬虫的论坛数据分析系统的设计与实现(华中科技大学·黎曦)
- 基于网络爬虫的论坛数据分析系统的设计与实现(华中科技大学·黎曦)
- 基于结构数据的多模式智能问答消歧系统(山东大学·李华东)
- 基于矩阵相乘的需求追踪方法及技术支持(广西师范大学·王超)
- 基于MapGIS的地图服务系统的设计与实现(中国地质大学·汪鹏)
- 基于B/S结构的新闻发布系统(吉林大学·郭蕊)
- 基于结构数据的多模式智能问答消歧系统(山东大学·李华东)
- 基于行列转换的统计功能研究与应用(中国海洋大学·张娜)
- 基于深度学习的智能问答系统的研究与实现(沈阳师范大学·卓越)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕业设计驿站 ,原文地址:https://bishedaima.com/yuanma/36032.html











