求解多极小函数
求解多极值函数问题中,我们需要求出函数的最值,我们以函数 f(x0,x1) = x1sin(x0) x0 cos(x1) 为例,求它在 x0,x1 ∈ [10,10] 区间内的最小值。
使用 MATLAB 画出的函数图像如图 1 所示,其最小值可用 matlab 库函数求出,约为-17.394,同时该函数有多个局部极小值。

图 1: 函数 f(x) 图像
SA 算法
算法流程
如步骤图 2、参数设置图 3、流程图 4,步骤 1 中,初始温度可以有两种生成方式:按照经验设定固定初温或随机选择指定数量的状态计算目标值并把方差作为初温;初始解在连续函数中为函数值。
步骤 2 中,在外循环中,温度随着迭代而发生变化,收敛准则分为基于时间的收敛(指定迭代次数,需要指定迭代次数)和基于性能的收敛(连续若干步的目标值之差小于阈值,需要指定阈值和迭代步数)。
步骤 3 中,抽样稳定准则是在内循环中用来决定同一个温度下产生解的个数,温度不随着内循环迭代而发生改变。收敛准则分为基于时间的收敛(指定迭代次数,需要指定迭代次数)和基于性能的收敛(连续若干步的目标值之差小于阈值,需要指定阈值和迭代步数)。
步骤 4 为状态更新,在连续函数的优化问题中,需要指定自变量更新的步长和移动长度的分布类型(高斯分布或柯西分布其中退温为对外循环的温度进行降温,分为指数退温(需要指定温度衰减系数)和对数退温。
步骤 5 为状态判断,如果新解的目标值更优,则用它来替换当前解,否则保持当前状态不变,并继续循环。

图 2: 模拟退火算法流程

图 3: 模拟退火算法参数设置
2.1.2 次随机实验的统计结果
由于可选择的参数较多,这里的演示为指定了部分模式和参数来进行比较。不建议使用基于优化的收敛准则,因为需要指定阈值和迭代步数,在未知目标值范围的情况下随意迭代难以找到理想的解,有可能无法跳出循环。(改进思路:或许可以采用自适应阈值的算法。)
如图 1.1.2, 修改外循环迭代次数,依次为 50、100、150。在状态转换步骤中,即使新状态并非最优,也有一定的概率可以跳转到新状态上。在这里,外循环迭代次数设置得不宜过高,因为最终温度会变得非常小,导致跳转概率的计算超过计算机所能存储的 64 位,故在退温步骤中设置温度不能小于 1e-4。
在迭代次数为 50 时,20 次循环也找不到最小值;迭代次数为 100 和 150 时能够找到最小值,说明适当增加迭代次数有助于进行更大范围的搜索;但 150 次的平均性能未必比 100 次好,找到的最差解和平均解都不如 100 次。这可能是因为在循环中设置了温度的下限,在 (130,150] 次中进行迭代时,温度一直被限制在 1e-4, 使得在出现了性能并非更优的解时的跳转概率很大,即无论解如何都要跳转,导致性能相对于 100 次时发生下降。
2.1.3 目标函数的变化曲线
如图 8,算法在 35 个回合之后趋向于收敛。

图 4: 模拟退火算法流程图

图 5: 外循环迭代 50 次

图 6: 外循环迭代 100 次
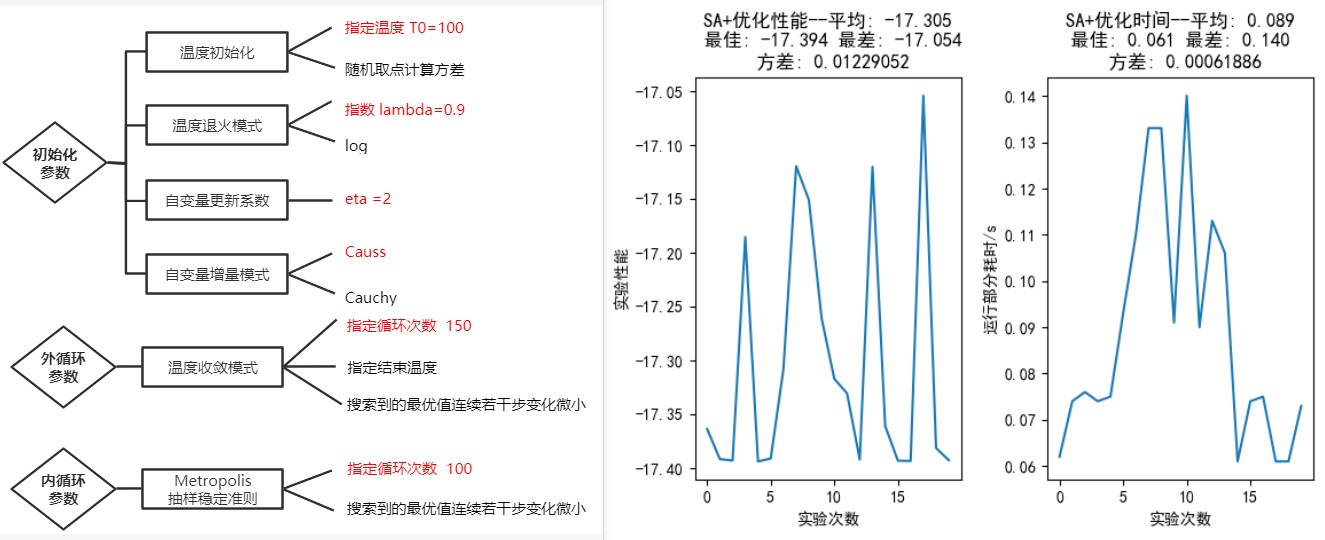
图 7: 外循环迭代 150 次

图 8: 连续优化问题,SA, 目标函数的变化曲线
GA 算法
编码
遗传算法需要对问题的解进行编码,对此,我们使用 32 位二进制码表示问题的解,前 16 位表示 x0,后 16 位表示 x1。x0,x1 的取值范围都为 [10,10],使用 16 位二进制码表示可以使解精确到小数点后 3 位。二进制码 [S]2 与实数 x 的关系为:

算法流程
算法流程与标准的 GA 算法相同,步骤与课件中相同,如图 9 所示。其中,适配值为函数值。
在产生新种群时,步骤 5 之前,先将上一代种群排序,保留一部分较优个体,再从中生成下一代种群。

图 9: 遗传算法流程
算法的选择步骤中,我们使用基于排名的方法,先将种群个体按适配值排名,以线性关系给每个排名的个体分配一个概率值,然后归一化。倒数排名为 i 的个体被选择的概率值为
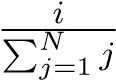
此外,选择操作之前,父代种群中的适配值最高的两个个体会直接继承到子代种群。
交叉操作中,我们对 x0 染色体和 x1 染色体分别进行交叉。为交叉一对染色体,我们随机产生一个交叉点,交换该点左右的基因,生成一对新染色体。变异操作中,我们对染色体中的每个基因(01 二进制数)按变异概率进行随机改变。
我们采用保优操作,即保存算法出现过的适配值最高的解。如果保优值在若干回合中一直保持不变,认为算法收敛,提前结束迭代,同时我们也有最高迭代次数的限制。
算法参数
- 最大迭代次数:2000
- 种群规模:30
- 交叉概率:0.95
- 变异概率:0.1
- 保优值保持不变提前结束迭代的回合数:100
- 产生新种群时先从上一代种群选出一部分较优个体,其比例:1.0
次随机实验的统计结果
统计结果如图 10 所示,平均性能: 17.394,最佳性能: 17.394,最差性能: 17.393,方差:
。
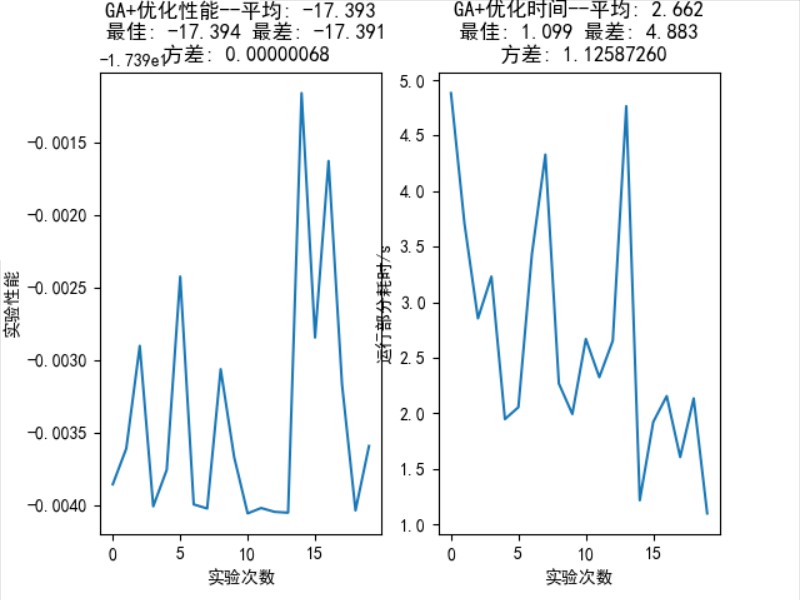
图 10: 函数优化问题中,GA 算法 20 次随机实验的统计结果
目标函数的变化曲线
在一次实验中目标函数的变化曲线如图 11 所示。
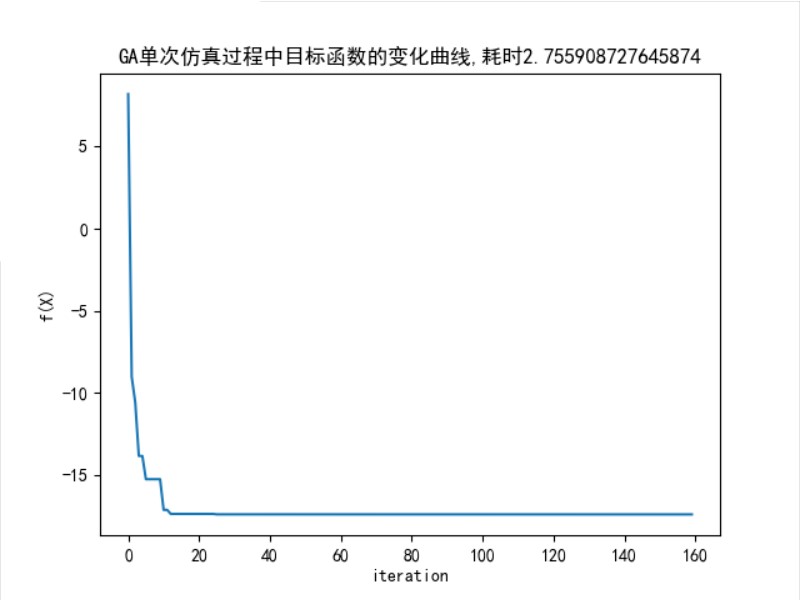
图 11: 函数优化问题中,GA 算法目标函数的变换曲线
TSP 问题
我们以网络学堂中 TSP30 文件中的点信息做测试。
SA 算法
算法流程
算法流程与上文基本类似,不同之处在于:
步骤 1 中,初始温度可以有两种生成方式:按照经验设定固定初温要更大,随机选择指定数量计算方差时指定的元素数目也大得多;初始解在离散的 TSP 问题中为旅行商所经城市的路线。
步骤 4 为状态更新,在 TSP 问题中,可以通过进行两位置元素交换、两位置之间的元素逆序、把指定某一段序列插到第三个位置之后或者把上述操作按照概率混合的方法产生新的状态,即新的旅行商路线。
次随机实验的统计结果
30个城市:
最短距离为 423.74,0.7-3.6s 可找到最优解。
如图 12,从上到下依次指定外循环迭代 100 次、内循环迭代 200 次;外循环迭代 100 次、内循环迭代 400 次;外循环迭代 200 次、内循环迭代 400 次;外循环迭代 200 次、内循环迭代,所有参数的设置见图像 12 左半部分。
在外循环迭代 100 次、内循环迭代 200 次中,虽然随机 20 次实验中能够找到最优解(距离 423.741), 但从图中可以看出这样的次数并不多,且距离方差很大。增大内循环迭代次数到,明显在 20 次实验中找到最优解的次数增加,距离方差也变小很多。
在外循环迭代 200 次、内循环迭代 400 次中,20 次随机试验中能够找到最优解的次数高于外循环迭代 100 次、内循环迭代 400 次;而将内循环迭代次数继续提高到 500 次时,性能又有了明显提升——最差距离与最优解仅仅相差不到 2 个单位,方差迅速降低到 0.24。
上述实验说明,在一定范围之内提高迭代次数有利于提升性能,但迭代次数设置得是否合理,是需要结合初始温度来进行考虑。迭代次数越多耗时越长,需要在性能与耗时方面做出权衡。
50个城市:
最短距离为 428.10,0.9-9.6s 内可找到最优解。
如图 13,参数设置与 30 个城市基本相同,仅改变内外循环次数进行实验。从上到下依次为外循环 100 次、内循环 200 次;外循环 100 次、内循环 400 次;外循环 200 次、内循环 400 次;外循环 200 次、内循环 1000 次。图中右半部分为 20 次实验中的最优路径,均没有发生路径交叉。随着迭代次数的增加,搜寻到的最短路径在减小,平均搜寻路径和方差也在减小,运行时间在增加。但由于状态更新的随机性,有时候未必能够得到性能优化。
75个城市:
最短距离为 544.20,37-173s 内可找到最优解。
如图 14,从上到下依次为初始温度 700、外循环迭代 200 次、内循环迭代 3000 次;初始温度 700、外循环迭代 200 次、内循环迭代 5000 次; 初始温度 700,温度收敛到 1e-5、内循环迭代 5000 次。图中左侧为 20 次实验所得结果,右图为每 20 次实验的最短路径。到了 75 个城市时,使用之前的参数已经无法获取最优解,因此需要进行参数调整。为了增加搜寻的路径范围,此时设置的参数值较 TSP30、TSP50 有大幅度增加。尽管如此,搜寻到最优解的概率仍然很小,运行多次也只能得到一次 544.20,连 546、547、548 这样的数值都很少能够搜寻得到。
总结:
在 50 个城市与 75 个城市中,由于城市较多,形成闭合路径的方法有很多,此时已经无法通过目测来判断每 20 次实验的最优解是否为最短路径。增加内循环次数的本质是在状态转换概率没有太大改变的情况下增加尝试的路径,以便尽可能覆盖较优解。增加外循环次数的本质是改变解的跳转概率,能够跳出局部最优,继续寻找全局最优解。
随着城市数量的增加,问题的复杂度变得很高,每次实验的运行时间变得很长,更难以搜寻到最优解,也无法通过肉眼判断是否搜寻到了最优,因为每次实验的路径都没有出现交叉。如图 15,随着问题规模的增长,距离开始明显下降的迭代次数开始上升 (TSP30 在 25 前后,TSP50 在 30-40 之间,TSP75 在 30-40 之间),距离趋向于收敛的次数也在上升 (TSP30 在 50 之前,TSP50 在 50-60 之间,TSP75 大于 60)。说明盲目增大外循环迭代次数意义不大。问题规模对于 SA 算法的影响很大,在较复杂的问题下,SA 性能并不算理想;中小规模下 SA 算是一种兼顾了时间和性能的算法。
注:实验表明,在产生新状态的过程中,新状态应当基于前一个产生的新状态而不是当前状态来产生,即使前一个新状态没有被接受,不能成为当前状态。这样运行多次,新状态与当前状态将有较大不同,更有可能找到最优路径。若所有新状态都是基于当前状态产生,则路径
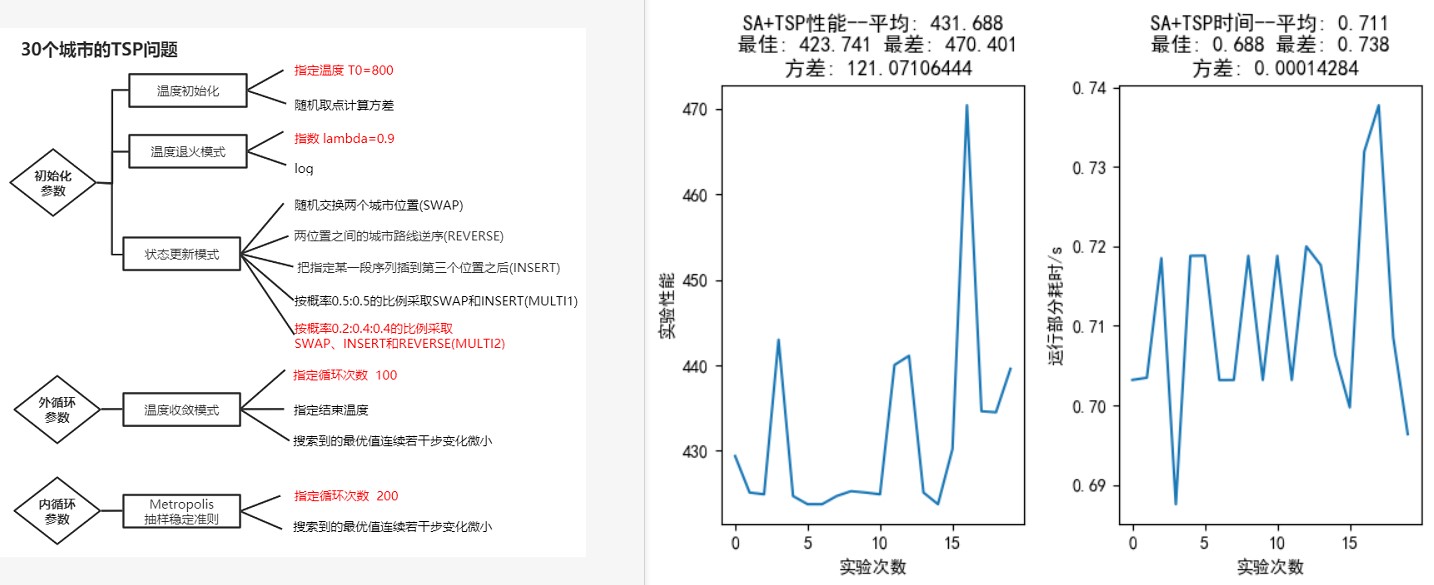



图 12: TSP30,SA 算法
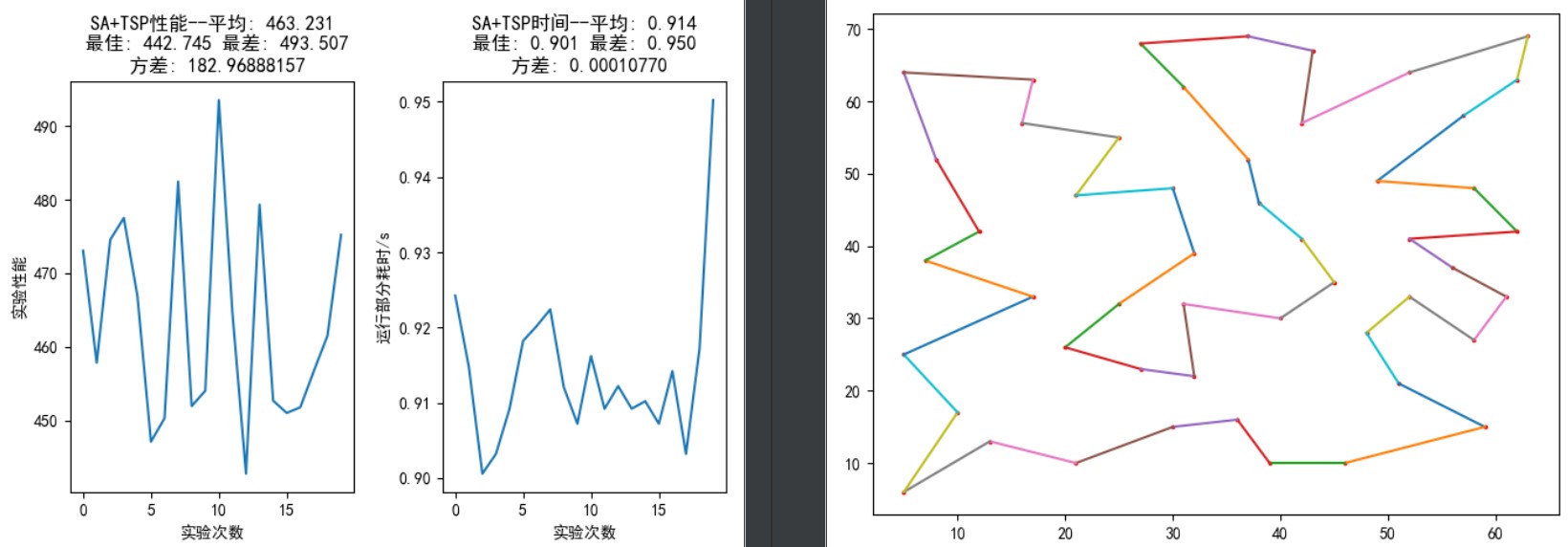
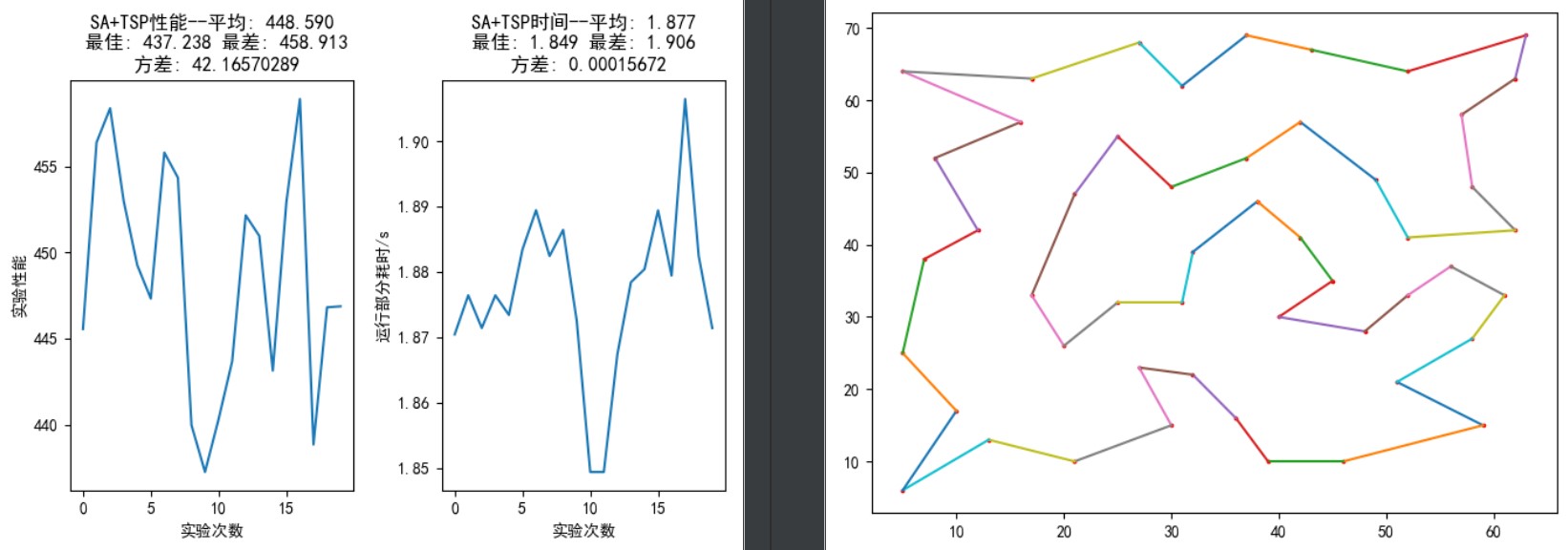
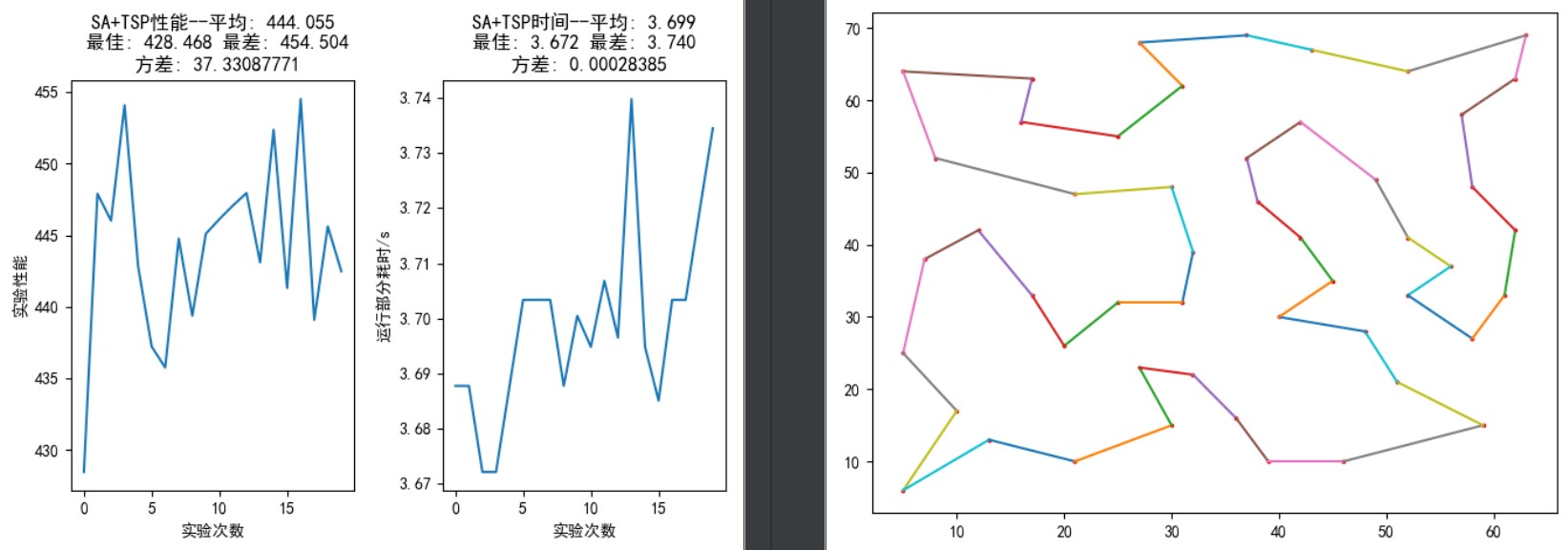

图 13: TSP50,SA 算法

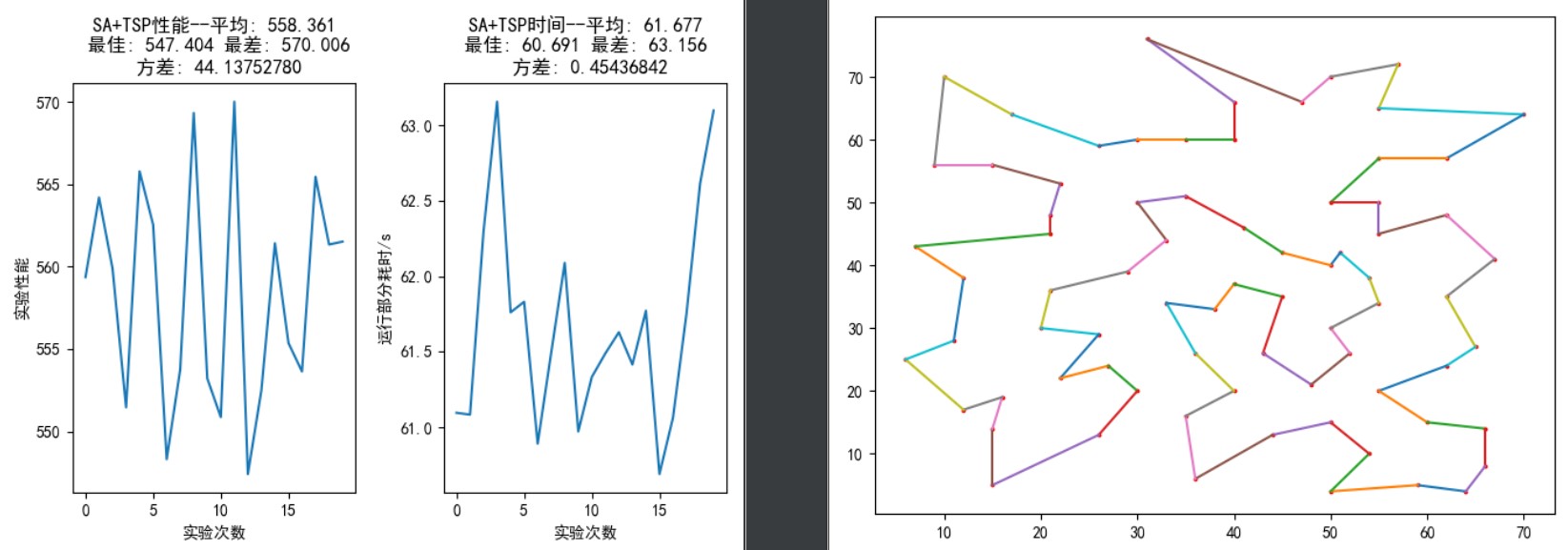

图 14: TSP75,SA 算法
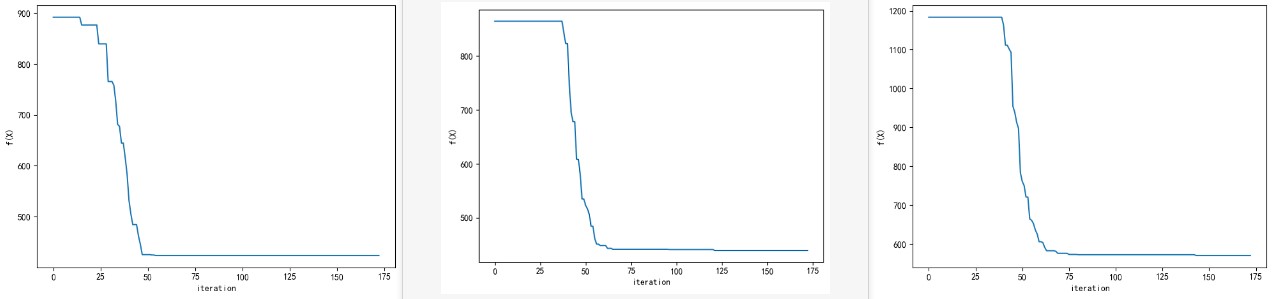
图 15: TSP30、50、75 最短距离随着外循环迭代次数的变化是否变短会十分依赖于初始产生的路径,多次迭代也相当于只在当前路径上尝试小的城市变动,路径很难缩短,难以找到最优。
GA 算法
编码
用路径顺序进行编码,比如 5 个城市路径:[4,2,3,0,1]。
算法流程
- 算法流程与前一问题中描述的流程相同。
- 对于交叉操作,我们尝试了部分映射交叉和单位置次序交叉两种方法,实验发现单位制次序交叉方法的性能更优。
- 变异操作中,我们对染色体中的每个基因(某城市)按变异概率随机与路径中另一城市交换次序。
- 与函数优化问题相同,我们在该问题中同样采用保优操作。
算法参数
- 最大迭代次数:2000
- 种群规模:60
- 交叉概率:0.95
- 变异概率:0.2
- 保优值保持不变提前结束迭代的回合数:500
- 产生新种群时先从上一代种群选出一部分较优个体,其比例:0.2
次随机实验的统计结果
个城市的统计结果如图 16 所示,平均性能: 441.690,最佳性能: 423.741,最差性能:
,方差: 281.369。
个城市的统计结果如图 16 所示,平均性能: 456.699,最佳性能: 430.346,最差性能:
,方差: 135.855。
个城市的统计结果如图 16 所示,平均性能: 593.437,最佳性能: 567.233,最差性能:
,方差: 250.265。
次实验结果
在某次实验中,目标函数(总距离)变化过程如图 19 所示。
最优结果的总距离为 423.741,路径图如图 20 所示,路径顺序如图 21。
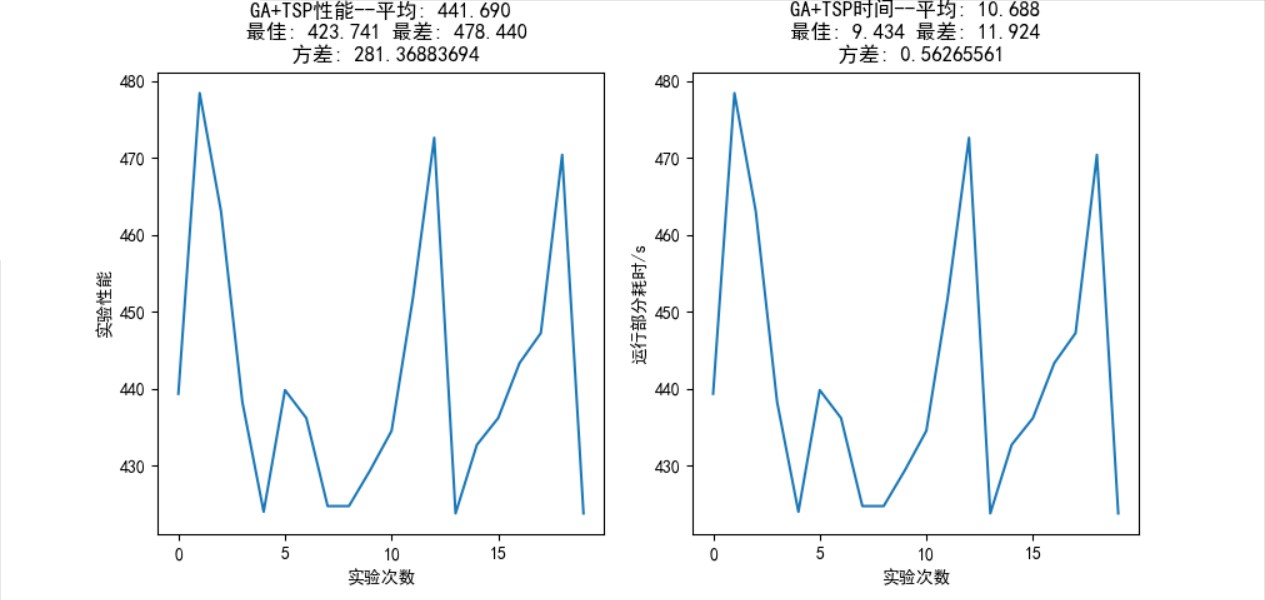
图 16: TSP 30 个城市问题中,GA 算法 20 次随机实验的统计结果
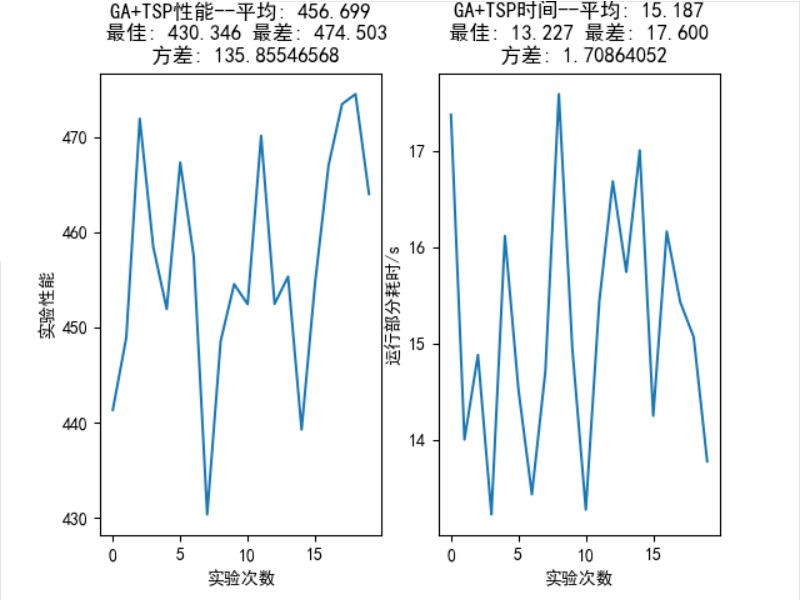
图 17: TSP 50 个城市问题中,GA 算法 20 次随机实验的统计结果
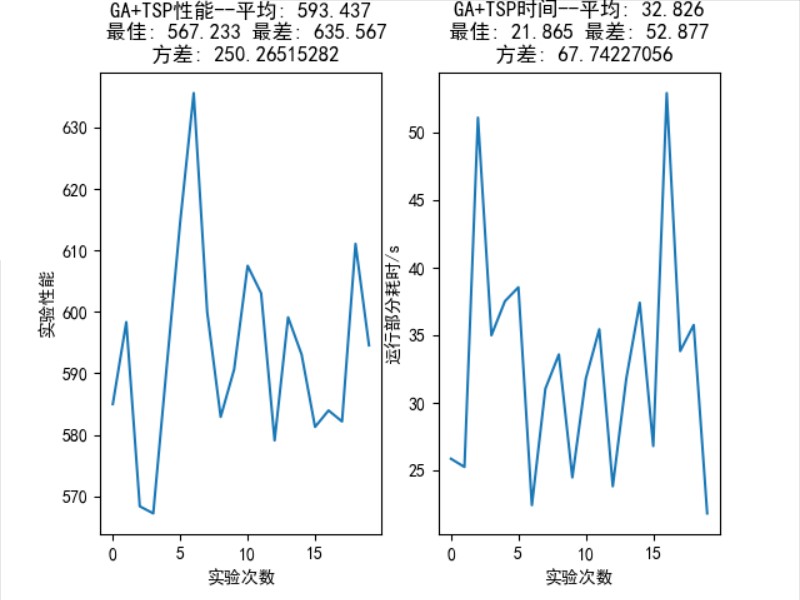
图 18: TSP 75 个城市问题中,GA 算法 20 次随机实验的统计结果
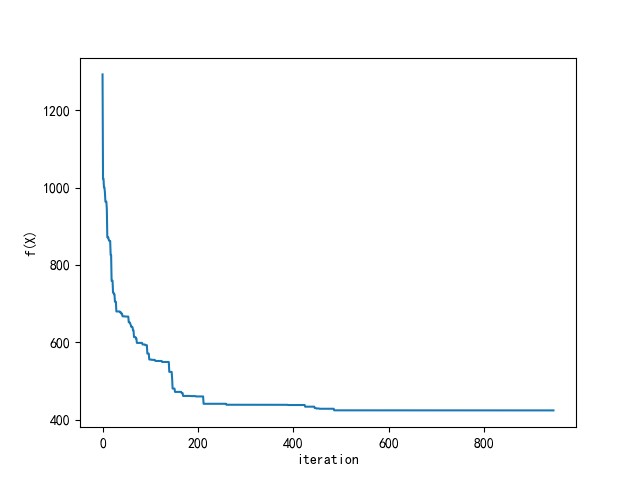
图 19: TSP 问题中,GA 算法一次实验目标函数的变化

图 20: TSP 问题中,GA 算法最优结果的路径图

图 21: TSP 问题中,GA 算法最优结果的路径
算法特点
SA
- 有概率突跳性,能够以一定概率接受较差的解,从而跳出局部最优,找到全局最优解。
- 串行运行,当问题规模较大时,运行时间显著增加。
- 是一种迭代寻优的方法,运行性能与迭代次数密切相关。
- 是一种随机寻优方法,最优解能否找到与问题规模相关,具有较大随机性。
GA
- 算法通过模仿自然界中遗传进化的模式,来实现寻优,适用范围较广,在离散优化问题和连续优化问题中都能使用。
- 是一种并行算法,多个个体同时搜索,易于实现算法的并行化处理。
- 由于遗传算法使用多个个体同时搜索,所以算法不易陷入局部极值点,寻优能力较强。
- 可以通过控制算法的变异交叉概率来平衡算法的全局搜索能力和局部探索能力,变异交叉概率较高时,全局搜索能力较强,反之局部探索能力较强。
TSP 可视化应用程序
用途:用来显示单次实验中 TSP 路线随着迭代次数增加的实时变化情况。可以使用老师提供的 TSP30、50、75 个城市的 txt 文件,也可以随机生成指定点数的城市,如图 22

图 22: TSP 应用程序
应用程序的用法及其可执行文件的下载链接见 READEME.md 文件。
注:
由于 SA 可选模式较多,ui 难以呈现,故 ui 中仅显示 SA 算法基于迭代次数收敛的选项(也是最理想的参数设置方案)。
在 SA 中,状态更新模式对结果影响较大,默认模式为效果较好的 MULTI2;循环迭代次数对结果影响也很大。建议参数:TSP30/50(外循环 200 次、内循环 500 次)、TSP75(外循环次、内循环 3000 次)。
由于报告中的数据分析是在非 ui 界面下运行的 (main_TSP.py),与使用 ui(ui_TSP.py) 运行同一个算法的时间会有出入。
运行非 ui(Optimization-algorithm-main/main_TSP.py): 可改参数位于 394-422 行。运行 ui 可执行程序: 显示图形界面。
实验分工
SA 算法:周映佟
GA 算法:吾尔开希
应用程序:吾尔开希 周映佟
参考文献
- 基于Python的非结构化数据检索系统的设计与实现(南京邮电大学·董海兰)
- 基于SSH2+AJAX架构的在线招聘求职系统设计与实现(吉林大学·李琦)
- 分布式统计信息基础数据库统计报表查询子系统的设计与实现(福州大学·曾瑾)
- 基于B/S的考卷搜索和标记系统的设计与实现(华中师范大学·沈亮)
- 基于矩阵相乘的需求追踪方法及技术支持(广西师范大学·王超)
- 基于J2EE的远程网络教育系统研究与实现(电子科技大学·陈南荪)
- 基于.NET平台的ETF终端设计与实现(吉林大学·刘健)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于SSH2+AJAX架构的在线招聘求职系统设计与实现(吉林大学·李琦)
- 基于B/S的考卷搜索和标记系统的设计与实现(华中师范大学·沈亮)
- 基于深度学习的智能问答系统的研究与实现(沈阳师范大学·卓越)
- 基于.NET的表格组件研究与实现(长沙理工大学·袁圣江)
- 基于粒子群算法的饮食规划系统研究(西安理工大学·吴记昌)
- 基于行列转换的统计功能研究与应用(中国海洋大学·张娜)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码工厂 ,原文地址:https://bishedaima.com/yuanma/36028.html











