CryptographyLab
编译并运行
```bash git clone git@github.com:Kiprey/CryptographyLab.git cd CryptographyLab
cmake . -B build
cd build
make -j
nproc
pip3 install --user PySide6 pip3 install --user pwntools pip3 install --user ctypes
cd ../src/Modern_GUI_PyDracula_PySide6_or_PyQt6 python3 main.py ```
编译方式
使用
cmake . -B build
创建 Makefile。
编译结果将保存在 build 文件夹下。
Cmake 可选参数:
bash
-DASAN_ENABLE=True # 启动漏洞检测机制,在检测到越界读写等开发漏洞时,立即 abort
-DCMAKE_BUILD_TYPE=Release # 发行版编译,启动优化技术
调试开发时,个人推荐使用以下命令进行编译:
bash
cmake . -B build -DASAN_ENABLE=True -DCMAKE_BUILD_TYPE=Debug
cd build
make
SSL 使用
首先,使用 openssl 分别创建证书:
```bash
生成服务端私钥
openssl genrsa -aes128 -out server.key 1024 (带加密的密钥生成)
openssl genrsa -out server.key
生成服务端证书签名请求文件
openssl req -new -key server.key -out server.csr
生成客户端私钥
openssl genrsa -aes128 -out client.key 1024 (带加密的密钥生成)
openssl genrsa -out client.key
生成客户端证书签名请求文件
openssl req -new -key client.key -out client.csr
生成 CA 签名文件
openssl genrsa -aes128 -out ca.key 1024 (带加密的密钥生成)
openssl genrsa -out ca.key
生成 CA 自签名证书
openssl req -new -x509 -key ca.key -out ca.crt
使用 CA 对服务端和客户端签名请求文件进行签名,创建对应的证书
-CA 用于签名的 CA CRT 证书
-CAkey 用于签名的 CA 密钥
-CAcreateserial 序列号文件不存在时自动生成
-in 等待被签名的 签名请求文件
-out 签名后生成的证书
openssl x509 -req -days 3650 -in server.csr -CA ca.crt -CAkey ca.key -CAcreateserial -out server.crt openssl x509 -req -days 3650 -in client.csr -CA ca.crt -CAkey ca.key -CAcreateserial -out client.crt
证书验证
openssl verify -verbose -x509_strict -CAfile ca.crt server.crt openssl verify -verbose -x509_strict -CAfile ca.crt client.crt ```
之后,执行 SSL_test 并根据输出进行输入即可正常使用。
运行 prequires
python 版本为 3.9.2,依赖安装:
````bash
项目Ui基于PySide6
pip install --user PySide6
pwn-tools开启线程
pip install --user pwntools
调用c++库
pip install --user ctypes ````
安装完成后在
CryptographyLab/src/Modern_GUI_PyDracula_PySide6_or_PyQt6
目录下运行
main.py
如果遇到 Asian 问题,执行
bash
export ASAN_OPTIONS=verify_asan_link_order=0
仿射加密算法
加密
c=key1*m+key2 (mod 26)
解密
m=(c-key2+26)*key1^(-1) (mod 26)
注意
- key1 必须和 26 互素,否则 key1 关于 26 没有逆元,算法不成立
- 之前要求 key2 小于 26,现在 key2 只需要大于等于 0 即可,因为实现时会让 key2=key2%26
- 放射加密只能处理 26 个字母,所有大写字母会被转换成小写字母加密,其它的字符会被忽略
DES 加解密算法设计说明
加解密概述
明文:任意长度的字符串。
密文:由 16 进制数字组成的字符串。
密钥:8 位字符。
DES.h
```c++ //DES.h
pragma once
include
include
using namespace std;
void generateKeys(string& k); // 生成子密钥 // 由于密文转字符容易乱码。故明文为普通字符串,密文为16进制数组成的字符串 string encrypt(string &s); // 加密函数 string decrypt(string &s); // 解密函数 ```
单次加解密
特征
分组加密算法:明文和密文为 64 位分组长度;
对称算法:加密和解密除密钥编排不同外,使用同一算法;
密钥长度:64 位,但每个字节第 8 位为奇偶校验位,可忽略;
密钥可为任意的 56 位数,但存在弱密钥,尽量避开;
采用混乱和扩散的组合,每个组合先替代后置换,共 16 轮;
只使用了标准的算术和逻辑运算,易于实现。
流程图
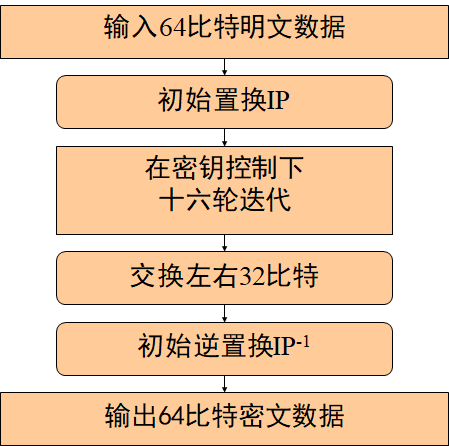
单次加解密函数代码(以加密为例)
c
// 单次DES加密(64位)
string encryptOnce(string s)
{
bitset<64> plain = charToBitset(s.c_str());
string result;
bitset<64> temp_cipher;
bitset<64> current_bits;
bitset<32> left;
bitset<32> right;
bitset<32> new_left;
// 第一步:初始置换IP
for (int i = 0; i < 64; ++i)
current_bits[63 - i] = plain[64 - IP[i]];
// 第二步:获取 Li 和 Ri,进行十六轮迭代(乘积变换)
for (int i = 32; i < 64; ++i)
left[i - 32] = current_bits[i];
for (int i = 0; i < 32; ++i)
right[i] = current_bits[i];
for (int round = 0; round < 16; ++round)
{
new_left = right;
right = left ^ f(right, g_sub_key[round]);
left = new_left;
}
// 第三步:合并L32和R32,注意合并为 R32L32
for (int i = 0; i < 32; ++i)
temp_cipher[i] = left[i];
for (int i = 32; i < 64; ++i)
temp_cipher[i] = right[i - 32];
// 第四步:初始逆置换IP^(-1)
current_bits = temp_cipher;
for (int i = 0; i < 64; ++i)
temp_cipher[63 - i] = current_bits[64 - IP_1[i]];
// 返回密文
return temp_cipher.to_string();
}
初始置换 IP 和 IP^(-1)
作用:将 64 位明文打乱重排
乘积变换(核心部分)
原理
将经过 IP 置换后的数据分成 32 bit 的左右两组;
每次迭代时只对右边的 32 bit 进行一系列的加密变换,在此轮迭代即将结束时,把左边的 32 bit 与右边得到的 32 bit 逐位模 2 相加,作为下一轮迭代时右边的段;
将原来右边未经变换的段直接送到左边的寄存器中作为下一轮迭代时左边的段;
在每一轮迭代时,右边的段要经过选择扩展运算 E、密钥加密运算、选择压缩运算 S、置换运算 P 和左右混合运算。
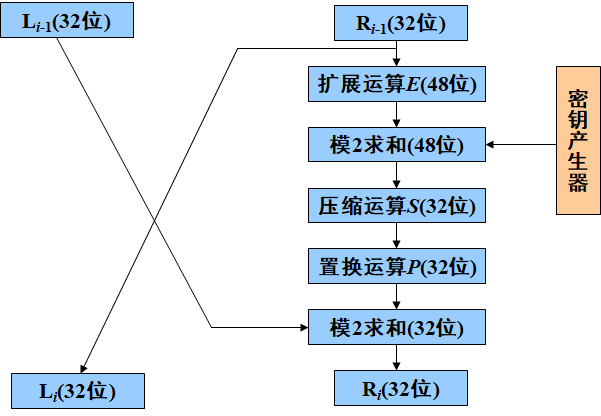
乘积变换函数代码
c
//乘积变换f,接收32位数据和48位子密钥,产生一个32位的输出
bitset<32> f(bitset<32> R, bitset<48> k)
{
bitset<48> expandR;
// 第一步:选择扩展运算E,32->48
for (int i = 0; i < 48; ++i)
expandR[47 - i] = R[32 - E[i]];
// 第二步:异或(模2相加)
expandR = expandR ^ k;
// 第三步:选择压缩运算S,48->32
bitset<32> output;
int x = 0;
for (int i = 0; i < 48; i = i + 6)
{
//首位2位决定行,中间4位决定列
int row = expandR[47 - i] * 2 + expandR[47 - i - 5];
int col = expandR[47 - i - 1] * 8 + expandR[47 - i - 2] * 4 + expandR[47 - i - 3] * 2 + expandR[47 - i - 4];
int num = S_BOX[i / 6][row][col];
bitset<4> binary(num);
output[31 - x] = binary[3];
output[31 - x - 1] = binary[2];
output[31 - x - 2] = binary[1];
output[31 - x - 3] = binary[0];
x += 4;
}
// 第四步:置换运算P,32->32
bitset<32> tmp = output;
for (int i = 0; i < 32; ++i)
output[31 - i] = tmp[32 - P[i]];
return output;
}
选择扩展运算 E
作用
通过置换表 E,将输入的 32 bit R i-1 扩展成 48 bit 的输出
原理
令 s 表示运算 E 原输入数据比特的原下标,则运算 E 的输出是将原下标 s =0 或 1(mod 4)的各比特重复一次得到的,即对原第 32, 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29 各位都重复一次,实现数据扩展。
模 2 求和
将子密钥产生器输出的 48 bit 子密钥 k i 与选择扩展运算 E 输出的 48 bits 数据按位模 2 相加。
子密钥产生器
原理
在 64 bit 初始密钥中有 8 位为校验位,其位置号为 8、16、32、48、56 和 64。其余 56 位为有效位,用于子密钥计算。
置换选择 PC1:将这 56 位送入置换选择 PC_1 进行坐标置换;
循环移位置换:将上述结果分成两组 28 bit,分别送入 left 和 right 中。在各次迭代中,left 和 right 分别将存数进行左循环移位置换;
置换选择 PC2:每次移位后,将 left 和 right 寄存器原存数送给置换选择 PC_2。置换选择 PC_2 将 left 中第 9、18、22、25 位和 right 中第 7、9、15、26 位删去,并将其余数字置换位置后送出 48 bit 数字作为第 i 次迭代时所用的子密钥 ki。
函数代码
c
// 生成16个48位的子密钥
void generateKeys(string &k)
{
bitset<64> key = charToBitset(k.c_str()); // 64位密钥
bitset<56> realKey;
bitset<28> left;
bitset<28> right;
bitset<48> compressKey;
// 去掉奇偶标记位,将64位密钥变成56位
for (int i = 0; i < 56; ++i)
realKey[55 - i] = key[64 - PC_1[i]];
// 生成子密钥,保存在 subKeys[16]中
for (int round = 0; round < 16; ++round)
{
// 前28位与后28位
for (int i = 28; i < 56; ++i)
left[i - 28] = realKey[i];
for (int i = 0; i < 28; ++i)
right[i] = realKey[i];
// 左移
left = leftShift(left, shiftBits[round]);
// 右移
right = leftShift(right, shiftBits[round]);
// 压缩置换,由56位得到48位子密钥
for (int i = 28; i < 56; ++i)
realKey[i] = left[i - 28];
for (int i = 0; i < 28; ++i)
realKey[i] = right[i];
for (int i = 0; i < 48; ++i)
compressKey[47 - i] = realKey[56 - PC_2[i]];
g_sub_key[round] = compressKey;
}
}
示意图
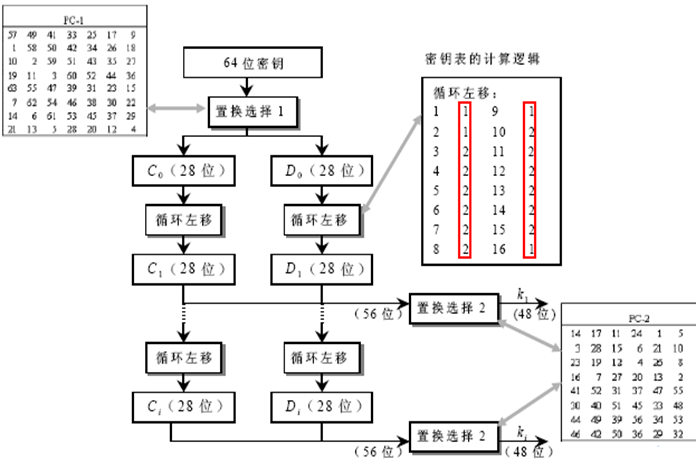
压缩置换 S
原理
将前面送来的 48 bit 数据自左至右分成 8 组,每组为 6 bit;而后并行送入 8 个 S 盒,每个 S 盒为一非线性代换网络,有 4 个输出。
示意图
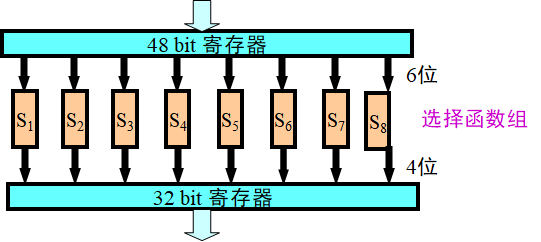
置换运算 P:
作用
通过置换表 P,对 S 1 至 S 8 盒输出的 32 bit 数据进行坐标置换。
DH 协议
一、密钥协商
在 Client 和 Server 建立连接后,
- Client 和 Server 建立自己的 RSA 公钥私钥,并生成自己的 DH 私钥,确定相同的 DH 公共参数 P 和 M。
- 双方交换公钥
- Client 使用 Server 公钥 对 自己的 DH 公钥 进行加密,并将加密后的值发送给 Server。Server 使用自己的私钥进行解密,获取到 Client DH 公钥。
- 之后 Server 重复 第三步,将自己的 DH 公钥以安全方式加密发送给 Client 并被对方解密获取。
- 双方根据自己的 DH 私钥和对方的 DH 公钥,求出共享密钥。
二、消息收发
消息收发需要支持
消息完整性验证(md5)
消息来源验证(数字签名 RSA)
对于发送方而言,需要发送 $E(m)|Sig(H(m))$信息,以进行 消息签名 与 完整性验证 ,同时保证 消息保密 。因此需要
使用共享密钥加密 m, 生成 E(m)
对明文 m 计算其哈希值 H(m),并使用自己的 RSA 私钥对该 H(m) 进行签名,得到 Sig(H(m))
将上述两步的结果进行拼接得到待发送数据,并将其发送
对于接收方而言,接收方需要验证发送来的信息的可用性:
根据 RSA 密钥长度,将接收到的信息分为密文和签名两部分,并分别使用共享密钥和对方的公钥进行解密,得到 m' 和 H'(m)
使用得到的 m' 计算哈希值 H(m'),判断其值是否等于远程发来的 H'(m),如果相同则说明消息可用,将其返回给上层应用程序。
LFSR-JK 触发器
LFSR
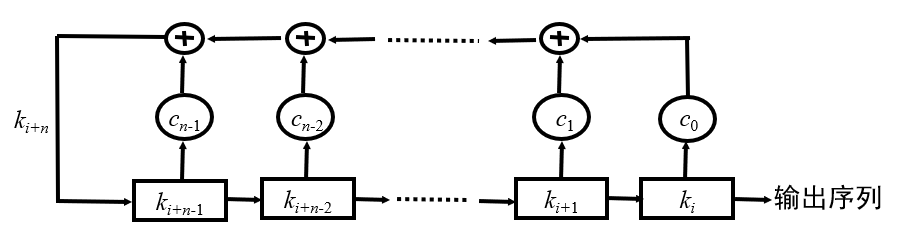 k 为移位寄存器
k 为移位寄存器
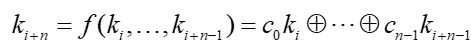 c 为反馈系数
例如:
如果 c0=1,c1=1,c2=0,c3=1
k0=1,k1=0,k2=0,k3=1
输出 k0=1,则新的 k3=c0 * k0 ⊕ c1 * k1 ⊕ c2 * k2 ⊕ c3 * k3=0
c 为反馈系数
例如:
如果 c0=1,c1=1,c2=0,c3=1
k0=1,k1=0,k2=0,k3=1
输出 k0=1,则新的 k3=c0 * k0 ⊕ c1 * k1 ⊕ c2 * k2 ⊕ c3 * k3=0
JK 触发器
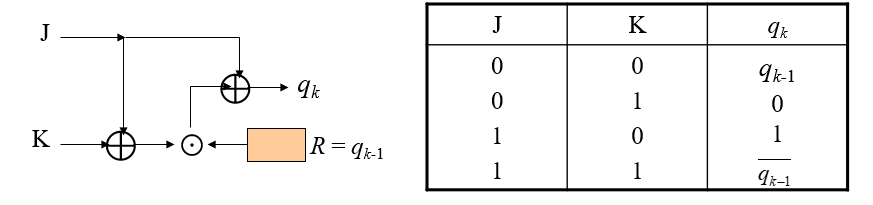 将两个 LFSR 的输出序列作为 JK 触发器的输入,JK 触发器的输出作为密钥流即可
将两个 LFSR 的输出序列作为 JK 触发器的输入,JK 触发器的输出作为密钥流即可
注
LFSR 并没有讲怎么用密钥控制密钥流,所以我自己想了一个: ①key 四个字符为一组,各组异或结果的最低位(0 或 1)为四个反馈系数初始值; ② 不足四个字符的密钥:最低位重复填充四个系数; ③ 密钥按四个字符一组分组后剩下的字符:最低位依次和四个系数或,然后赋值给系数
两组 LFSR 四个寄存器初始值如下:
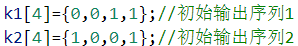
可加密任意字符串,密钥为任意字符串
RC4 加密算法
算法
- 初始化 S 盒
S[256]:S 盒是 char 型数组,大小为 256,填充[0,255]
k[256]:不断重复密钥填充数组 k,k[i] = key[i % len]
对于 i=0-255:j = (j + S[i] + k[i]) % 256,交换 s[i]和 s[j]
- 伪随机序列的生成
创建两个计数器 i,j,初始值为 0
i = (i + 1) % 256,j = (j + s[i]) % 256,交换 s[i]和 s[j]
下标 t = (s[i] + s[j]) % 256
- 加密/解密
s[t]^data
说明
可加密任意字符串,密钥为任意字符串
RSA 加解密算法设计说明
加解密概述
明文:任意长度的字符串
密文:由 5 位一组的十进制数字组成的字符串
密钥:公钥(e,n),私钥(d,n)。加密时自动生成,解密时用户输入。
RSA 体制的组成部分
密钥生成
加密
解密
RSA.h
```c
pragma once
include
include
using namespace std; //公钥(e,n),私钥(d,n) 规定模数不超过16位,即最多为5位十进制 struct key { int e; int d; int n; }; key ProduceKey(); //产生密钥 string publicEncrypt(string s, key k); //RSA公钥加密,生成密文:5位一组的十进制数字 string privateDecrypt(string s, key k); //RSA私钥解密,生成明文:字符串 string privateEncrypt(string s, key k); //RSA私钥加密,作签名,生成密文:5位一组的十进制数字 string publicDecrypt(string s, key k); //RSA公钥解密,作验证,生成明文:字符串 ```
密钥生成
- 首先选取两个大素数 p 和 q ,计算 n = pq ;
- 随机选取加密密钥 e ,使 e 和( p - 1)( q - 1)互素;
- 用扩展欧几里德算法计算解密密钥 d ,以满足:
- $ ed = 1mod(p - 1)(q - 1) $,即$ d = e-1mod(p- 1)(q - 1)$
- 公开钥为( e , n ),秘密钥为( d , n )。
函数代码
c
//产生密钥
key ProduceKey()
{
key k;
g_p = RandomlyGeneratePrime(3, 65536 / 128, 1);
g_q = RandomlyGeneratePrime(3, 65536 / g_p, 1); //使k.n=g_p*g_q不超过2^16
k.n = g_p * g_q;
unsigned int t = (g_p - 1) * (g_q - 1);
k.e = RandomlyGeneratePrime(2, t, t); //产生2到t-1的一个素数,且与t互质
k.d = CalculateD(k.e, t);
return k;
}
产生素数函数
c
//产生a到b-1的素数,且与t互质
unsigned int RandomlyGeneratePrime(unsigned int a, unsigned int b, unsigned int t)
{
unsigned int e = 0;
srand((unsigned int)time(0)); //设置随机数种子
e = a + rand() % (b - a - 1); //产生随机数e,从e开始找素数作为我们随机生成的素数
do
{
if (e >= b) //若该素数大于b-1,重新生成一个随机数
{
e = a + rand() % (b - a - 1);
}
if (JudgePrimeNum(e) && RelativePrime(e, t)) //判断e是否为素数,且与t互质
{
break;
}
} while (e++);
cout << e << endl;
return e;
}
求模函数
c
//通过(a*a)%n =((a%n)*a)%n求(a^b)%n
unsigned int PowerModule(int a, int b, int n)
{
unsigned int result = 1;
while (b--)
{
result = (result * a) % n;
}
return result;
}
公钥解密,私钥解密
公钥加密
- 数学变换:$C=M^emodn$
- C:明文
- M:密文
- (e,n):公钥
c
//RSA公钥加密,生成密文:5位一组的十进制数字
string publicEncrypt(string s, key k)
{
string result = "";
int len = s.length();
for (int i = 0; i < len; i++)
{
int temp = PowerModule(s[i], k.e, k.n); //字符串中的每个字符对应一个5位数字
int dividend = 10000;
while (dividend) //将5位数字转化为字符加入结果
{
result += (temp / dividend + '0');
temp %= dividend;
dividend /= 10;
}
}
return result;
}
私钥解密
- 数学变换:$M=C^dmodn$
C:明文
M:密文
(d,n):私钥
c
//RSA私钥解密,生成明文:字符串
string privateDecrypt(string s, key k)
{
string result = "";
int len = s.length();
for (int i = 0; i < len; i += 5)
{
string single = s.substr(i, 5);
unsigned int c = 0;
int factor = 10000;
for (int j = 0; j < 5; j++)
{
c += factor * (single[j] - '0');
factor /= 10;
}
int temp = PowerModule(c, k.d, k.n);
result += (char)temp;
}
return result;
}
私钥加密,公钥解密
- 做签名和验证
私钥加密
- 数学变换:$C=M^dmodn$
C:明文
M:密文
(d,n):私钥
c
// RSA私钥加密,作签名,生成密文:5位一组的十进制数字
string privateEncrypt(string s, key k)
{
string result = "";
int len = s.length();
for (int i = 0; i < len; i++)
{
int temp = PowerModule(s[i], k.d, k.n); //字符串中的每个字符对应一个5位数字
int dividend = 10000;
while (dividend) //将5位数字转化为字符加入结果
{
result += (temp / dividend + '0');
temp %= dividend;
dividend /= 10;
}
}
return result;
}
公钥解密
数学变换:$C=M^emodn$
C:明文
M:密文
(e,n):公钥 e
c
// RSA公钥解密,作验证,生成明文:字符串
string publicDecrypt(string s, key k)
{
string result = "";
int len = s.length();
for (int i = 0; i < len; i += 5)
{
string single = s.substr(i, 5); //5位数字对应一个字符
unsigned int c = 0;
int factor = 10000;
for (int j = 0; j < 5; j++)
{
c += factor * (single[j] - '0'); //将5位数字的字符串转化位int型
factor /= 10;
}
int temp = PowerModule(c, k.e, k.n);
result += (char)temp;
}
return result;
}
SSL 通信
一、证书配置
配置三份私钥和证书,分别是
客户端的私钥和证书
服务端的私钥和证书
CA 的私钥和证书
并使用 CA 的私钥,分别对 客户端、服务端以及 CA 自己的公钥证书进行签名。
二、连接
在进行 SSL 通信之前,客户端和服务端必须配置好
自己的私钥路径
自己的公钥证书路径
可信任的 CA 公钥证书路径。CA 公钥证书用于验证对方是否是可信赖的
配置好后,双方先进行 socket 连接,连接之中不涉及 SSL。
连接完成后,使用 socket 的文件描述符初始化 SSL 对象,并调用 SSL 对象中的 connect 和 accept 方法。这两个方法会尝试进行 SSL 握手,验证对方的证书和等待被对方验证。如果验证失败则立即提醒并断开连接。
如果身份验证成功,则使用 SSL_read 和 SSL_write 函数进行通信。这两个函数底层会数据进行加密并在接收信息时自动完成一系列验证等。
参考文献
- 基于JSP的校园网站的设计与实现(吉林大学·张帆)
- 微课学习和管理平台的设计与实现(天津师范大学·宋晓婷)
- 基于Web系统的计算机编程语言书籍交流系统设计与开发(吉林大学·刘峰兵)
- VFP课程教学辅助系统的研究与设计(吉林大学·孙敏)
- 中学python课程知识图谱构建及应用研究(华中师范大学·黄健)
- 基于J2EE的远程教学管理系统的研究(南京信息工程大学·陈康)
- 校内课程师生互动系统的设计与实现(华南理工大学·李志毅)
- 基于PHP+MySQL的交互学习系统的设计与实现(吉林大学·刘博)
- 成人教育综合信息管理系统设计与实现(电子科技大学·伍家卫)
- 基于DWZ框架的培训学校管理系统的设计与实现(吉林大学·丛海洋)
- 基于B/S结构的网络选课系统设计与实现(黑龙江大学·陈天凯)
- 基于J2EE的远程网络教育系统研究与实现(电子科技大学·陈南荪)
- C语言程序设计精品课网站的设计与开发(大连理工大学·朱志刚)
- 精品课程网络平台的设计与实现(西安电子科技大学·乔小宇)
- C语言程序设计精品课网站的设计与开发(大连理工大学·朱志刚)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:毕业设计工坊 ,原文地址:https://bishedaima.com/yuanma/35979.html