美国国会投票记录实验报告
分析与设计
参考:
利用第三包。
详细实现

实验结果
{0} -> {-1} (conf: 0.990, supp: 0.462, lift: 0.995, conv: 0.467)
{1} -> {-1} (conf: 0.998, supp: 0.995, lift: 1.002, conv: 1.995)
{-1} -> {1} (conf: 1.000, supp: 0.995, lift: 1.002, conv: 2298850.575)
{republican} -> {-1} (conf: 0.994, supp: 0.384, lift: 0.999, conv: 0.772)
{0} -> {1} (conf: 0.995, supp: 0.464, lift: 0.997, conv: 0.467)
{republican} -> {1} (conf: 0.994, supp: 0.384, lift: 0.996, conv: 0.386)
{democrat} -> {-1} (conf: 0.996, supp: 0.611, lift: 1.001, conv: 1.228)
{democrat} -> {1} (conf: 1.000, supp: 0.614, lift: 1.002, conv: 2298850.575)
{0, 1} -> {-1} (conf: 0.995, supp: 0.462, lift: 1.000, conv: 0.929)
{-1, 0} -> {1} (conf: 1.000, supp: 0.462, lift: 1.002, conv: 2298850.575)
{0} -> {-1, 1} (conf: 0.990, supp: 0.462, lift: 0.995, conv: 0.467)
{1, republican} -> {-1} (conf: 1.000, supp: 0.384, lift: 1.005, conv: 4597701.149)
{-1, republican} -> {1} (conf: 1.000, supp: 0.384, lift: 1.002, conv: 2298850.575)
{republican} -> {-1, 1} (conf: 0.994, supp: 0.384, lift: 0.999, conv: 0.772)
{0, democrat} -> {-1} (conf: 0.993, supp: 0.326, lift: 0.998, conv: 0.657)
{1, democrat} -> {-1} (conf: 0.996, supp: 0.611, lift: 1.001, conv: 1.228)
{-1, democrat} -> {1} (conf: 1.000, supp: 0.611, lift: 1.002, conv: 2298850.575)
{democrat} -> {-1, 1} (conf: 0.996, supp: 0.611, lift: 1.001, conv: 1.228)
{0, democrat} -> {1} (conf: 1.000, supp: 0.329, lift: 1.002, conv: 2298850.575)
{0, 1, democrat} -> {-1} (conf: 0.993, supp: 0.326, lift: 0.998, conv: 0.657)
{-1, 0, democrat} -> {1} (conf: 1.000, supp: 0.326, lift: 1.002, conv: 2298850.575)
{0, democrat} -> {-1, 1} (conf: 0.993, supp: 0.326, lift: 0.998, conv: 0.657)
心得体会
使用了包,因此实验没有什么难度。之后或许会考虑自己实现。
利用层次聚类思想实现一个社区发现算法,在 karate 数据集上进行检测。
分析与设计
参考: Newman M E J, Girvan M. Finding and evaluating community structure in networks
算法采用 Girvan-Newman 算法,利用模块度 Q 作为寻找社区数量的依据。
Girvan-Newman 算法的基本流程如下:
计算网络中所有边的边介数;
找到边介数最高的边并将它从网络中移除;
重复步骤 2,直到每个节点成为一个独立的社区为止,即网络中没有边存在。

详细实现
使用 Python 编写代码
使用 networkx 作为实现网络的包
使用 matplotlib 绘制 Q 的变化
使用 gephi 查看图
构建 GN 类,其中有两个主要方法的划分方法:
GN.run(self):以 Q 最大作为划分依据
GN.run_n(self, n):当划分为 n 个时,停止划分
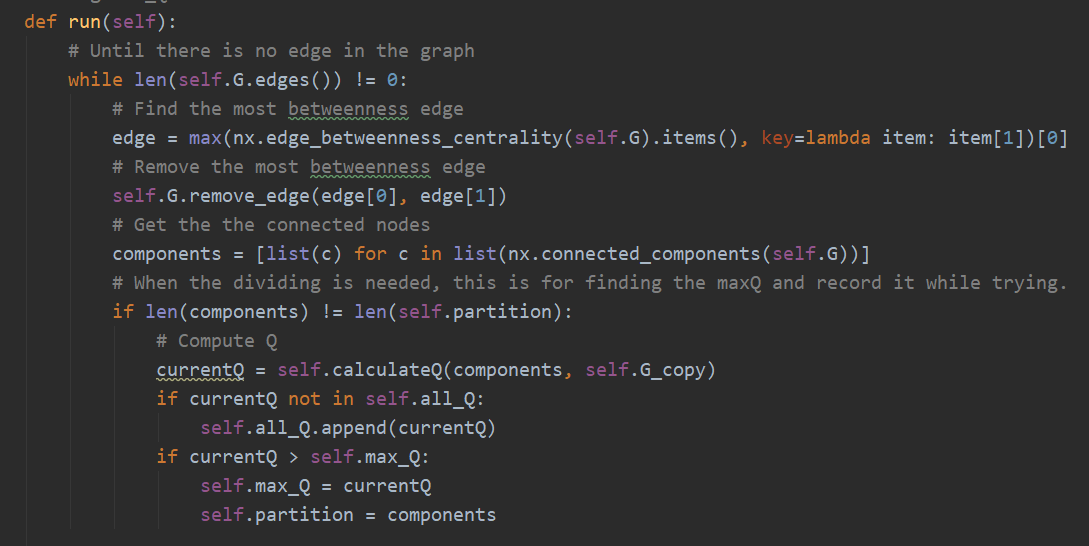
以 run 为例:一直去除介数最大的边,同时计算划分后的图的 Q 是否最大,如果最大,则以此图作为新的结果,否则继续划分。
GN.add_group(self):将原图的拷贝按照划分后的节点进行标记,方便之后的查看
GN.draw_Q(self):画出 Q 的变化趋势
GN. calculateQ(partition, G):计算目前的 Q
其余可参见代码:
结构如下:
- Main.py 程序实现
- /data:
- karate.gml:原始数据
- out.gml:依据 Q 最大划分结果
- two_parts.gml:依据两个社区划分结果
实验结果

参考文献
- 基于区块链的选举系统的设计与实现(郑州大学·鲁航)
- 股票数据库管理系统的设计与实现(电子科技大学·卢火)
- 基于区块链的选举系统的设计与实现(郑州大学·鲁航)
- 基于Android平台的手机投票系统(安徽大学·虞小湖)
- 政府民意调研分析系统设计与实现(东北大学·李树林)
- 基于SPRING MVC架构的数据同步系统的设计与实现(吉林大学·林薇)
- 基于区块链的选举系统的设计与实现(郑州大学·鲁航)
- 基于区块链的选举系统的设计与实现(郑州大学·鲁航)
- 基于区块链的选举系统的设计与实现(郑州大学·鲁航)
- 法官会议记录系统的设计与实现(南京大学·周川)
- 基于股票数据流和投资者情绪的股价预测系统的设计与实现(华南理工大学·陈泽铭)
- 广厦园林公司工程投标项目管理系统的设计与实现(山东大学·刘广辉)
- 一种多方匿名安全投票方案研究与设计(西安电子科技大学·孙京宇)
- 政府民意调研分析系统设计与实现(东北大学·李树林)
- 在线投票系统设计与实现(电子科技大学·周艳萍)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码客栈 ,原文地址:https://bishedaima.com/yuanma/35763.html











