基于Python实现种差值方法
一、种差值方法的实现与问题
三种插值方法都是使用Python自己实现的。
1.1 最近邻插值
寻找每个中心点周围的八个点中有无未丢失的点,如果有的话就赋值为第一个找到的点,如果没有就扩大范围再次寻找,在最大范围内都找不到的话就跳过。
1.2 双线性插值
使用解方程的方法求解,整体思路类似colorization作业的实现,每个点用周围的八个点线性表示,根据距离为1和确定两个权重。四个边界上的点只会由五个邻居来表示,每个权重为0.2,线性平均求和。构建稀疏矩阵,求解,A为权重的稀疏矩阵,x为一个通道上的像素点值,b为原图中保留的像素点的值。
1.3 径向基函数插值
确定一个邻域,根据邻域内的已知点,求解出rbf函数的参数w,然后使用w和这个径向基函数对邻域内的未知点进行拟合。算法有两个超参数——邻域大小、邻域移动的步长。邻域越大、步长越小计算结果越好,但是花费时间也越长。总共实现了以下六个rbf基函数。
三种算法都实现读取RGB通道的图像,将RGB转换成YUV进行运算,最后将结果转换为RGB图像进行展示、保存和评估。之所以进行转换是因为使用YUV可以保证所有的运算都是以float类型进行的,只在开始和结束进行两次转换,可以保证计算的正确性。一开始直接使用RGB通道进行计算,结果会出现异常,如下所示(90%的丢失率), 可能是由于中间int和float的类型转换导致的,因为统一使用YUV格式计算后问题就被规避了:

另外RBF插值中如果步长过大,会导致结果分块现象明显,下面是一个极端的情况,分块之间有一个像素点未被计算:

二、随机丢点的评估
使用RBF进行插值计算非常慢,所以选择了一幅较小的图片进行连续的评估,原图如下:

2.1 肉眼观察
以下分别是丢失率从0.1到0.9的修复结果,从左向右依次是bilinear、nearest、RBF(使用multiquadric 基函数):

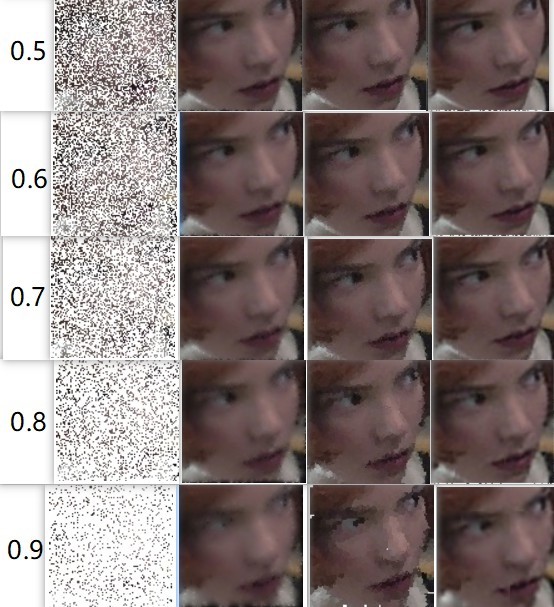
从上图的变化中可以看出在丢失率比较小的时候,三种算法并没有什么肉眼可见的差异,几乎都和原图相同。但是随着丢失率的上升,三种算法差异比较明显:
最近邻算法(中间)的结果变的模糊,并且有些走样,出现了原图中没有的结构双线性插值(左边)也有些模糊,但是看起来像是做过滤波平滑一样,但人脸结构都是正常的
c++
RBF插值(右边)的结果看起来比双线性的结果要清晰一些,也没有出现太多走样,但是有一些分块的边界比较明显,应该是因为设置的步长过大。下面在丢失率为90%时使用三种算法进行还原:


都能对图像做出不错的还原效果,但是最近邻插值会产生原本图像中没有的结构。
2.2 指标变化曲线
种算法比较 在上面的测试中,三种评价指标随丢失率增长的变化曲线如下所示:
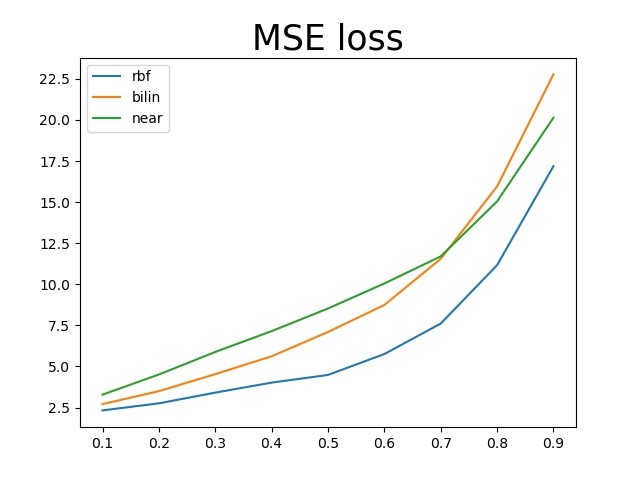
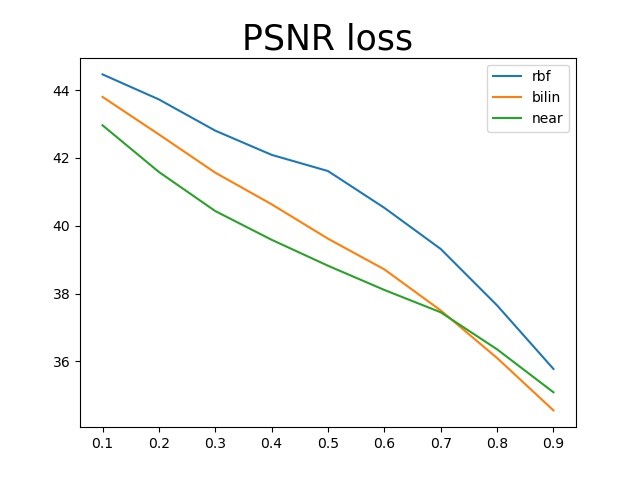
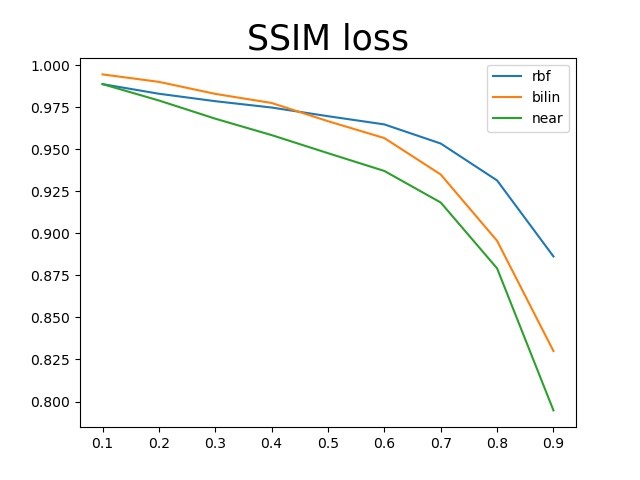
三种指标都可以看出RBF的结果最好,并且随着丢失率的增大,MSE增大、PSNR减小、SSIM减小的趋势也都是合理的。尤其是SSIM衡量结构相似性,在丢失率很小的时候三种算法都接近于1,这和上面肉眼观察的结果也是相同的。
RBF三种基函数比较
仍然是使用上面测试的那张图片,三种基函数中multiquadric和TPS的结果几乎是一模一样的,三个指标的曲线都是重合的,inverse quadric函数的结果要比另外两个差很多。
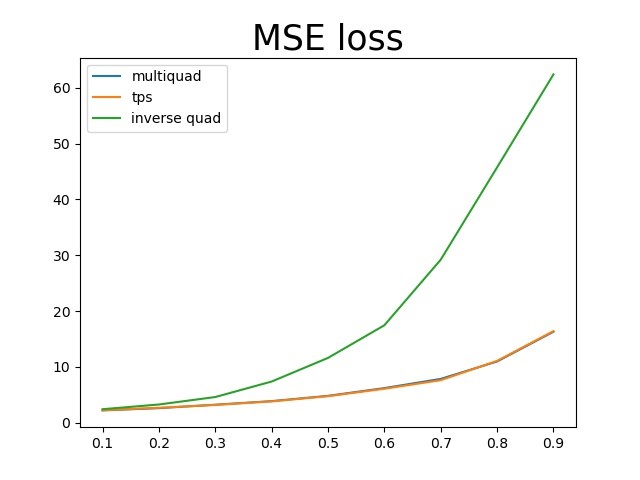
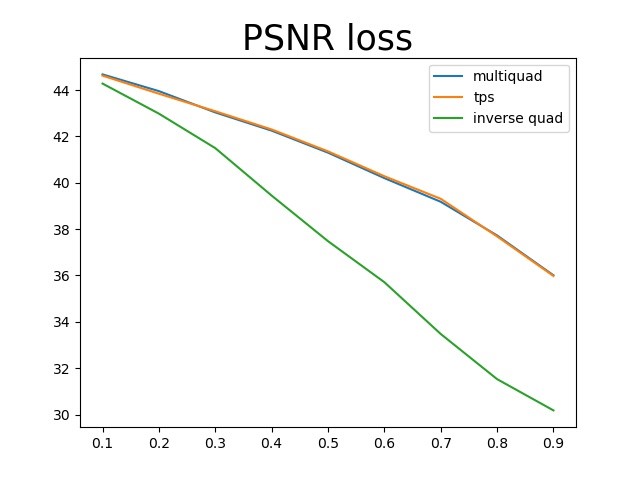
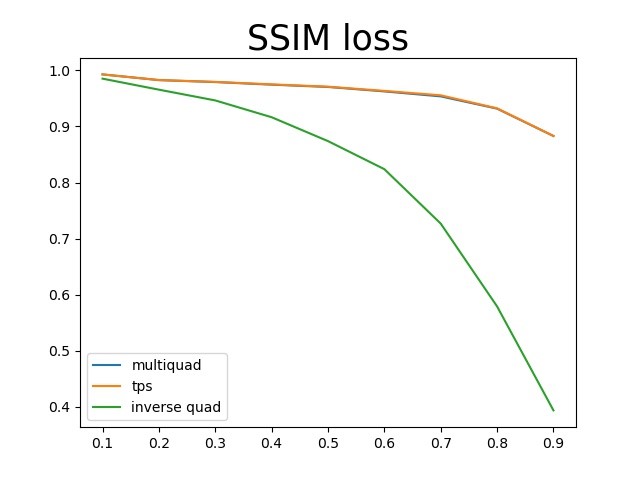
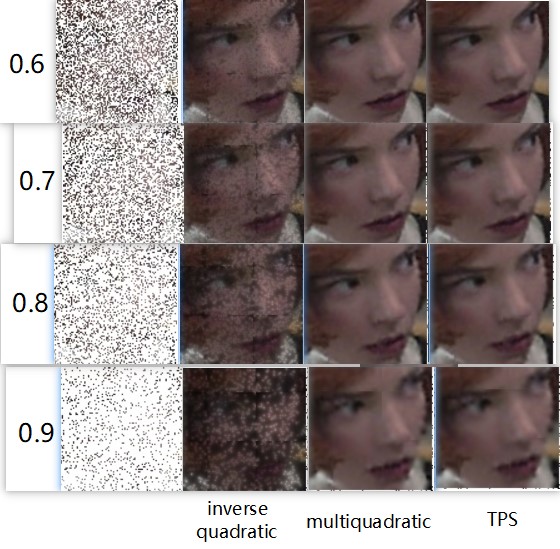
下面展示了丢失率在60%~90%时三种基函数对应的结果,很明显的可以看出inverse quadratic的效果非常差,还不如上面的最近邻插值,而另外两种基函数的结果没有太大差异,跟上面三种评价曲线的结果是一致的。
除了inverse quadratic函数之外,gaussian函数的效果也不好,这是因为修复的结果和径向基函数的系数是有关系的,而基函数中都默认为1,没有具体变化,所以导致有的基函数效果很差。

三、涂鸦、写字等破坏的评估
3.1 结果展示
对三幅图片分别进行了涂鸦、写字等破坏,修复结果如下:


显然最近邻算法的效果最差,都没能把涂鸦全都填起来,这应该是因为寻找的范围还不够大,有一些点正好处在全部都是空白的区域。另外两种的效果差不多,双线性修补结果更模糊一些,看起来效果甚至更好。


显然可以看出写字的修复效果要比画线的效果好得多,虽然一行字看着和涂鸦的宽度差不多,但是字母或者汉字并不是完全把小区域内的像素毁掉,而是留有一些缝隙,这些保留的缝隙正好可以起到很好的修复效果,所以就算是最近邻算法都有了比较好的表现。


可以看出仍然是最近邻算法的修复效果最差,尤其是对于画线的涂鸦部分,并且“董威龙”文字的部分修复效果也不好,因这个三个字笔画比较多,涂鸦效果基本和画线一样。bilinear和RBF效果差不多,涂鸦的部分虽然修复了,但是看着有一点模糊。
3.2 指标得分
以下是MSE、PSNR、SSIM三种损失评价的结果(MSE和SSIM使用Python提供的库,PSNR使用MSE结果自己计算):
c++
MSE
| 图一 | 图二 | 图三 | |
|---|---|---|---|
| RBF | 15.85 | 10.72 | 9.10 |
| bilinear | 14.42 | 10.96 | 9.29 |
| nearest | 15.68 | 10.79 | 9.07 |
c++
PSNR
| 图一 | 图二 | 图三 | |
|---|---|---|---|
| RBF | 36.13 | 37.82 | 38.54 |
| bilinear | 36.54 | 37.73 | 38.44 |
| nearest | 36.17 | 37.80 | 38.31 |
c++
SSIM
| 图一 | 图二 | 图三 | |
|---|---|---|---|
| RBF | 0.934 | 0.981 | 0.980 |
| bilinear | 0.948 | 0.975 | 0.978 |
| nearest | 0.881 | 0.970 | 0.961 |
3.3 极限测试


双线性插值在涂鸦部分是有所变化的,像是加上了一层半透明的蒙版效果,具有了图像本身的色调,这是因为双线性插值的算法是解一次方程得到整张图中一个通道的所有像素点信息,具有一定的全局性。
最近邻插值和RBF插值只是在一个局部邻域内进行计算,由于图片整个上半部分都被去除,邻域内没有任何已知点,所以得不到计算的结果,RBF略强于最近邻插值,在边界处图像有了一定的变化。
3.4 总结
查了一些近年来的图像修复算法,几乎全都是深度学习相关算法,并且大部分是基于CVPR 2016的Context-Encoders方法,使用了CNN+GAN,由于时间不够没有拿这些新的方法与作业中的方法对比。综合以上比较来看,双线性差值的效果应该是最好的,因为双线性插值的速度远快于RBF插值,这可能也跟RBF插值的实现不够“优雅”有关。并且对于相同算法,使用MATLAB的同学计算速度要比Python快一些,而且MATLAB的结果中MSE损失的数值平均比Python小一些,可能MATLAB对于数值计算有更好的优化。
参考文献
- NN-sort:学习型数据分布感知排序算法(云南大学·朱筱可)
- 基于行列转换的统计功能研究与应用(中国海洋大学·张娜)
- 棉花基差交易系统设计与实现(电子科技大学·石怡陶)
- 棉花基差交易系统设计与实现(电子科技大学·石怡陶)
- 基于J2EE的远程网络教育系统研究与实现(电子科技大学·陈南荪)
- 沪深A股选股系统的设计与实现(湖北工业大学·李凯)
- 基于区块链的模拟货币交易系统的设计与实现(北京交通大学·张星泽)
- 辽宁省农作物种质资源信息系统设计与开发(中国农业科学院·路明祥)
- 分布式网络爬虫在农产品搜索系统中的应用与研究(南昌大学·袁龙涛)
- J2EE和分布式数据库在军品价格管理交易系统中的应用(四川大学·朱剑涛)
- 空值关系模型在土地资源管理系统中的研究(太原科技大学·王新玲)
- 棉花基差交易系统设计与实现(电子科技大学·石怡陶)
- 分布式网络爬虫在农产品搜索系统中的应用与研究(南昌大学·袁龙涛)
- 数据挖掘算法的改进及应用研究(广西民族大学·路闯)
- 分布式网络爬虫在农产品搜索系统中的应用与研究(南昌大学·袁龙涛)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:代码工坊 ,原文地址:https://bishedaima.com/yuanma/36185.html