基于Python设计的吃豆人游戏
一、实现 Expectimax
期望最大(Expectimax)是在 MINIMAX 的基础上进行了概率的计算,这个最开始我还是很没有理解的,后来和叶老师与111173田鑫讨论后才悟了,如图 1:
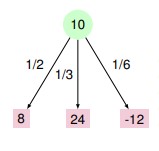
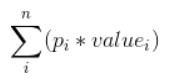
图 1 一颗普通的状态树 图 2 新的计算公式 这一层原本是 MINI 层,按照原来的算法,应该在其子节点中选择一个最小值传递到上一层,因此结果应该是-12。但现在添加了到达每个节点的概率,计算的方式就变成了求期望值,即图 2 的公式。其中 p 表示概率,value 该点的值。这样一来,该点的值就是 8 * 1/2+ 1/3 + -12 * 1/6 = 10,就不是之前的-12 了。
在吃豆人问题中,由于向每个方向走的概率都是相同的,因此只需要将子节点求和后除以合 action 的数量,就可以达到 Expecrimax 所描述的计算要求。
1.1 结果展示
通过对比AphasiaBeta和Expectimax对同一个地图进行测试,可以得到如下结果:
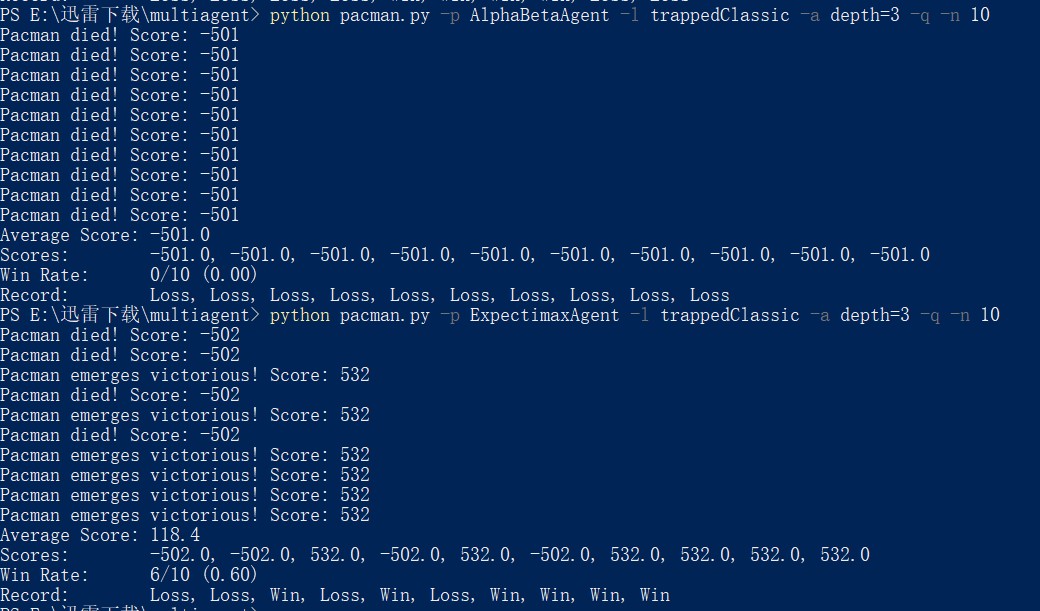
图 3 结果截图
可以看到相比之下,AphasiaBeta一场都没有赢过,而Expectimax赢了半数以上的对局,足以说明其策略更优。
二、实现 Reflex
在实现自定义评价函数的时候没懂是什么意思,因此和叶老师沟通后,开始着手做第一题。因为第一题也有自定义评价函数的内容,与第五题类似。Reflex中基本的思路就是
离食物越近越好
离鬼越远越好
因此评分标准就要围绕着上面两个思想来进行。首先离食物越近越好这个可以用倒数的形式来完成,而离鬼越远越好的话,我通过很长一段时间考虑…觉得用那种“离鬼越近负分越高”的评价会比较好,因此我决定用一个呈指数级别的函数,即 e的-x 次方。此时横坐标的x表示的就是吃豆人离鬼的距离。我们可以分析得到,当距离为0的时候是最危险的,因此其负的分数更高,如图5所示。
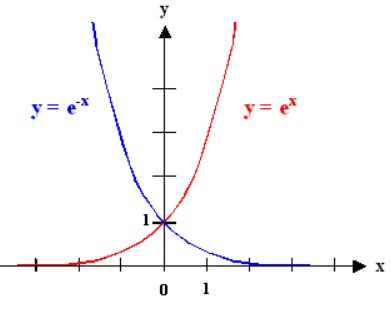

图 4 给我启发的 exp 的图象 图 5 最终使用的-exp 的图象
接下来的代码就比较玄学了,我直接(1/到最近食物距离)-exp(到鬼的距离),并且也尝试了很久调试参数,但是无论如何都不能使其运作的很好…最终我在github上参考了别人的代码,发现他也用的exp进行权值计算。但是他首先利用到了“oldFood”,用移动之前的食物记录,来判断当前这次有没有吃到食物,有的话就设置一个很高的分数,没有的话就设置为0。然后她也计算出了“到最近食物距离”和“到鬼的距离”,用刚才的分数减去这两个值。虽然不知道他咋想的,但这样确实管用…下面附上这位同学的代码链接:
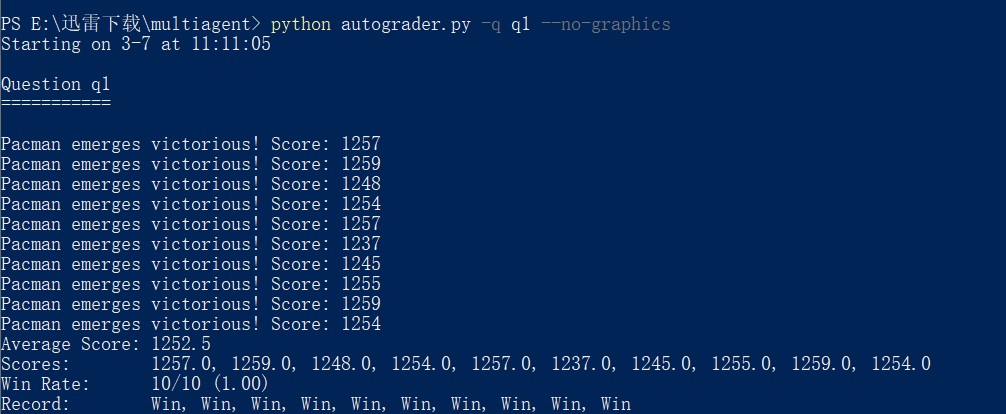
图 6 这位同学的精妙算法结果
三、实现 Evaluation Function
实现 Evaluation Function 的时候,我先按照自带的评价函数 scoreEvaluationFunction 直接计算 state 的得分,并作为评价值返回。运行结果如下:
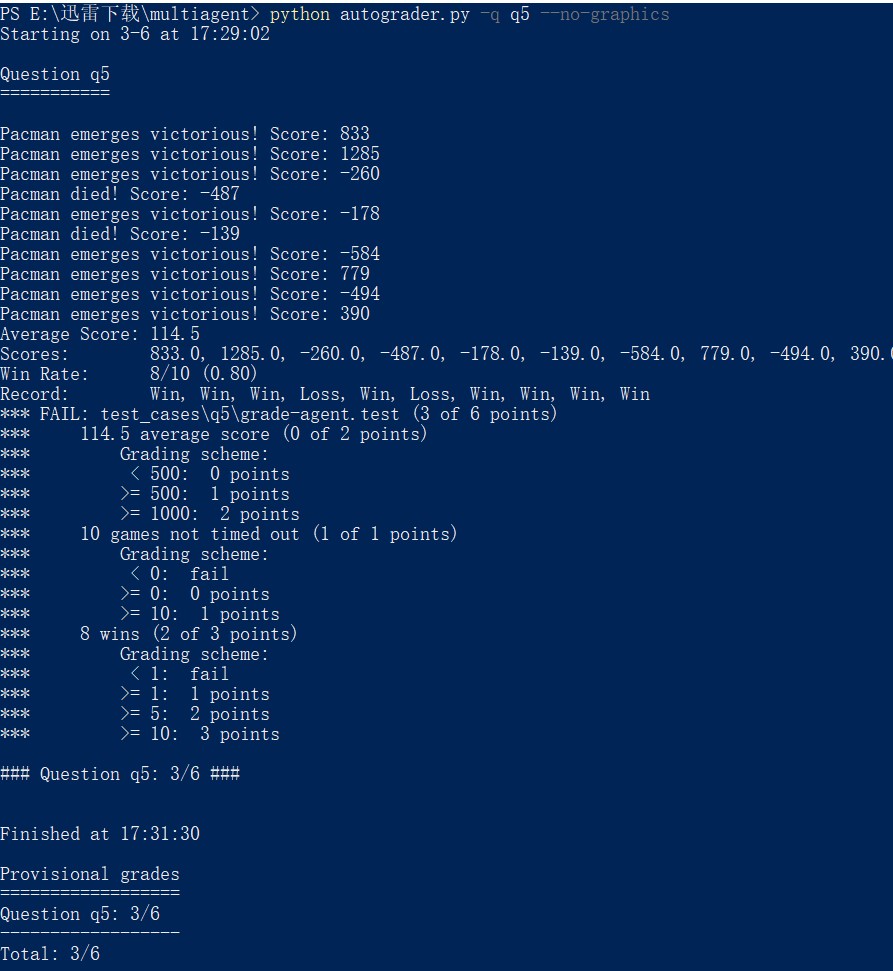
图 8 打印分数由于原来的评分功能已经很好的实现了正常吃豆和躲避鬼的代码,因此这里我添加了吃“药丸”的权重判断(在阅读源码的时候发现了 getCapsules 这个函数,可以获得地图中药丸的坐标)。在这个判断的规则下,吃豆人会更倾向于靠近药丸,并且在吃到药丸后,也更倾向于追逐鬼。这里我参考了 Reflex 中的计算方法,即计算得到曼哈顿距离后用 exp 计算获得一个较大的分数。
代码如下:

图 9 评价计算公式
这两段代码的计算方式十分相似,都是得到所有药丸/鬼的位置,然后计算曼哈顿得到一个最近的距离,对这个距离进行形如 math.exp(-(Value-5))的计算,便可得到评价值。需要说明的是,当吃豆人没有吃到药丸的时候,对鬼的分数依然是要打负分,因此有了图 9 中的那个 else 语句。
最终将原本的评分数值加上图 9 两个计算出来的两个值,就是最终的评分了,代码如下

图 10 最终评价计算
需要注意的是,这里加了一个小 tick:药丸得到的分数我乘以了 1.5 倍,因为如果不乘以这个系数的话,最终的平均得分是小于 1000 的,只能拿到这题的 5/6 分,如图 11:
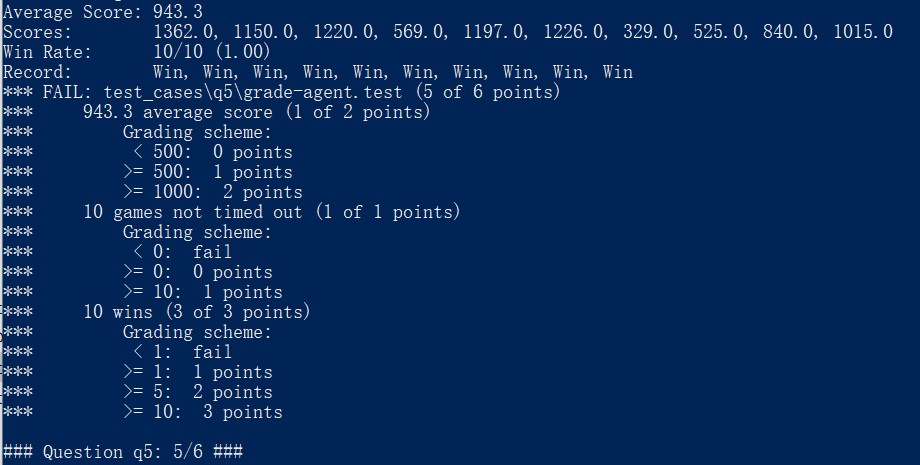
图 11 一次不太完美的结果
之所以乘以 1.5,这是在和111172周伟国同学讨论 Reflex 的时候他给我提供的思路,就是当好几个评分结果都影响最终得分的时候,可以设置权重系数,把你认为影响最大的那个结果通过系数放大,影响小的就通过系数变得更小。这样一来就能将局势判断朝你更倾向的那个思路进行下去。最终 PASS 的结果如图 12 所示:
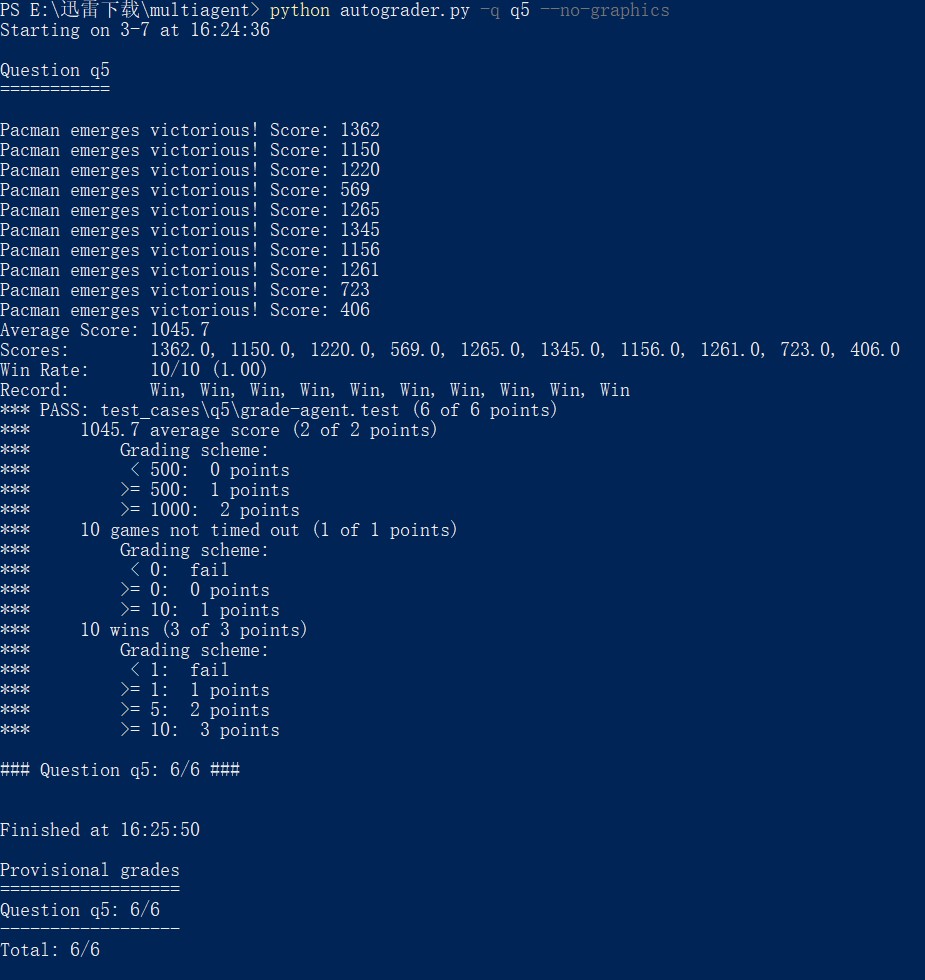
图 12 Perfect!
四、总结
学到的东西
想要放大距离对分数的影响可以用指数函数,其曲线满足分数距离越近越高,越远越低。同样的,也可以用系数来扩大分数的影响。
相比预测全部确定状态做出的决定,有时不如考虑随机性的因素而做出的决定
参考文献
- 基于轻量级J2EE的网络游戏虚拟物品交易系统的设计与实现(北京邮电大学·曹鹃)
- 基于手持移动设备的教学游戏设计与开发(上海师范大学·覃柳思)
- 面向高职信息技术教育的严肃游戏设计与实施(大连理工大学·王晓姝)
- 基于B/S架构的酷跑社区系统的设计与实现(内蒙古大学·张晓乐)
- 豆玩手机游戏平台的设计与实现(吉林大学·李天明)
- 网页游戏平台的管理与设计(哈尔滨师范大学·苏润泽)
- 网页游戏平台的管理与设计(哈尔滨师范大学·苏润泽)
- 面向计算思维发展的游戏创作学习活动设计与应用研究——以小学编程教学为例(华东师范大学·程亮)
- 基于web的旅游服务平台的设计与实现(内蒙古大学·张凡)
- 基于web的旅游服务平台的设计与实现(内蒙古大学·张凡)
- 教育类电子游戏设计与开发(上海交通大学·陶渊琛)
- 基于.NET平台的游戏门户系统设计与实现(电子科技大学·余胜鹏)
- 科学探究游戏的设计与应用研究——以《食品侦察队》为例(杭州师范大学·朱洲洋)
- 基于web的旅游服务平台的设计与实现(内蒙古大学·张凡)
- 基于Struts+JSP的SNS网站系统的设计与实现(吉林大学·王雷)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:代码导航 ,原文地址:https://bishedaima.com/yuanma/36180.html