1. 实验目的
掌握最小二乘法求解(无惩罚项的损失函数)、掌握加惩罚项(2 范数)的损失函数优化、梯度下降法、共轭梯度法、理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)
2. 实验要求
- 生成数据,加入噪声;
- 用高阶多项式函数拟合曲线;
- 用解析解求解两种 loss 的最优解(无正则项和有正则项)
- 优化方法求解最优解(梯度下降,共轭梯度);
- 用你得到的实验数据,解释过拟合。
-
用不同数据量,不同超参数,不同的多项式阶数,比较实验效果。
-
语言不限,可以用 matlab,python。求解解析解时可以利用现成的矩阵求逆。梯度下降,共轭梯度要求自己求梯度,迭代优化自己写。不许用现成的平台,例如 pytorch,tensorflow 的自动微分工具。
3. 实验内容
3.1 算法原理
本实验需要用多项式来拟合正弦函数。在 m 阶多项式中,有 m+1 个待定系数,m+1 个系数(由低到高)组成的(列)向量记作 w。要确定 w,用最小二乘法。
设 E(w) = 1/2 * (Xw – Y)^T(Xw – Y),其中,X 为多项式中各个未知项代入观测数据求得的矩阵,若记 Xi 为 X 的第 i 行的向量,则 Xi[j]为第 i 个观测数据 xi 的 j 次方,记有 n 组观测数据,多项式最高次为 m,易知 X 的维度为 n * (m+1)。Y 为观测标签向量。即 Y[j]为第 j 组观测数据的标签值(即 y 值)。从而问题转化为:求向量 w,使得 E(w)最小。
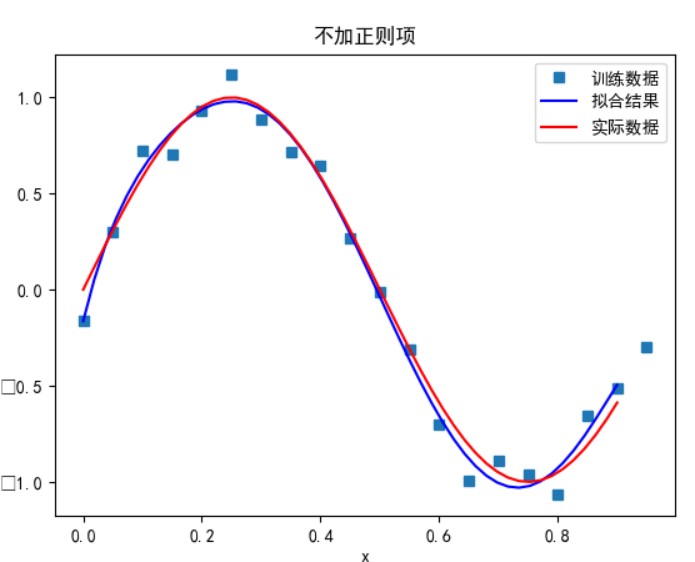
- 若不加入正则项,令损失函数导数为零,求 w
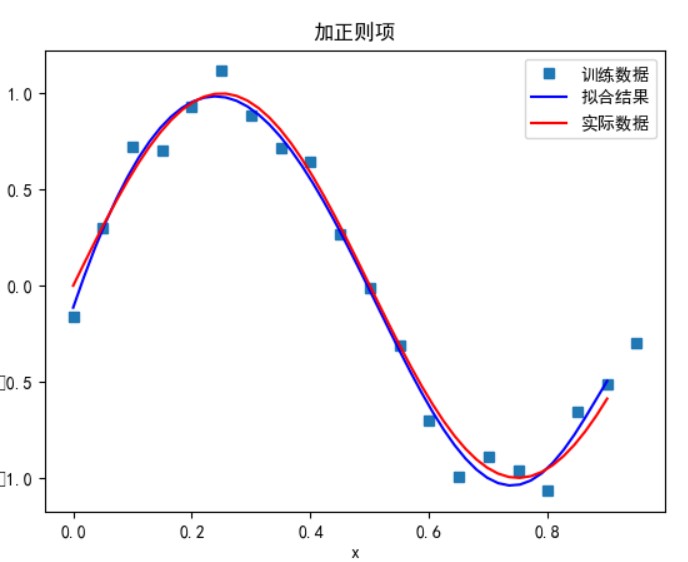
- 若加入正则项,令损失函数导数为零,求 w
- 加入正则项,对损失函数用梯度下降,当损失函数收敛时,求 w
- 加入正则项,对损失函数用共轭梯度法,循环迭代 m+1 次,求 w
3.2 算法实现
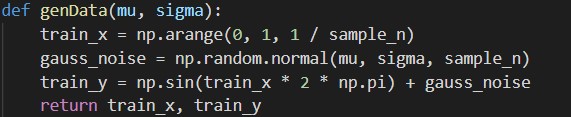
- 生成数据,加入噪声
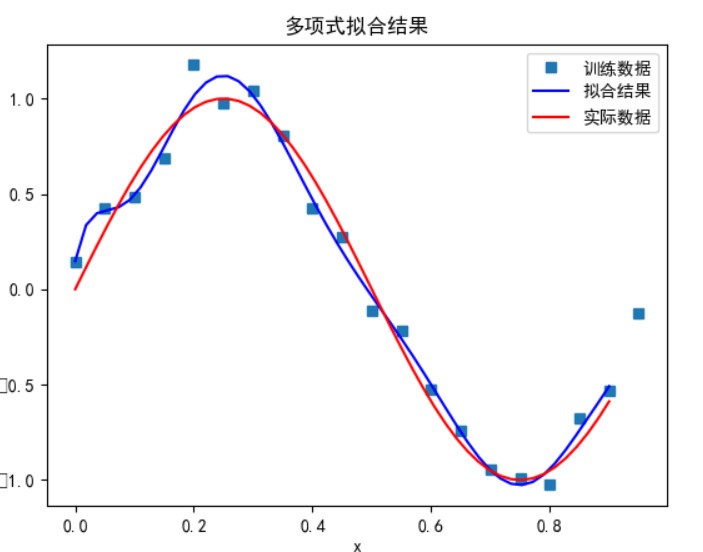
- 用高阶多项式函数拟合曲线;

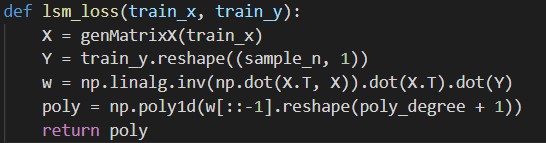
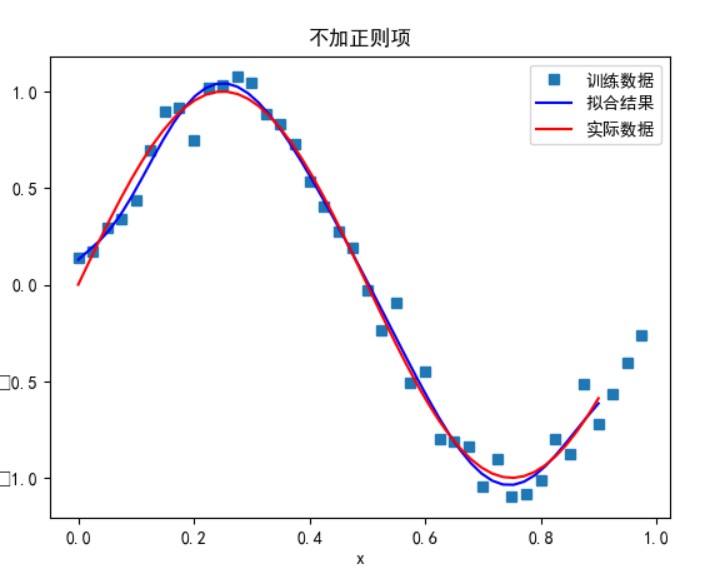
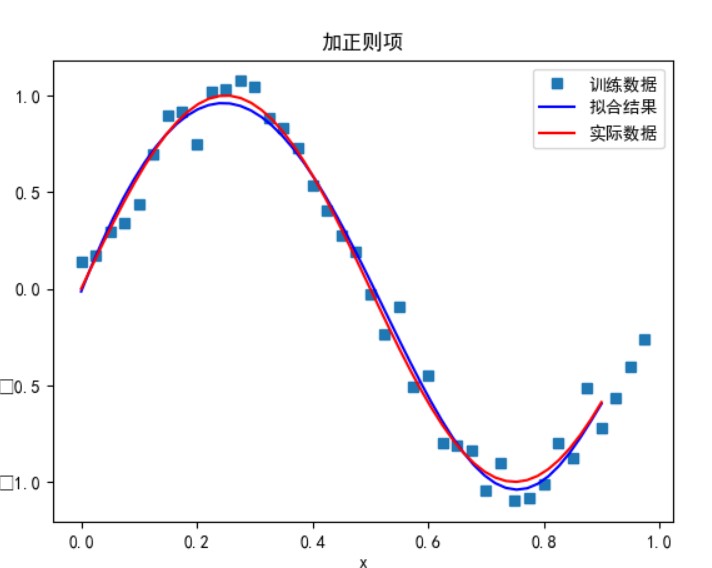
- 用解析解求解两种 loss 的最优解(无正则项和有正则项)
无正则项:
有正则项:

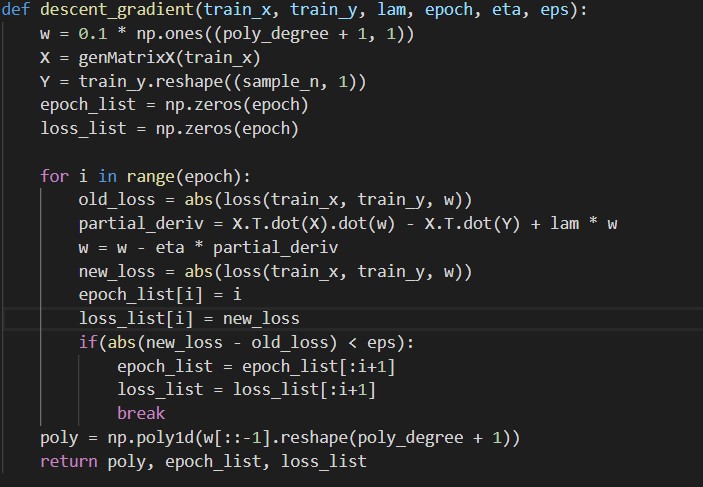
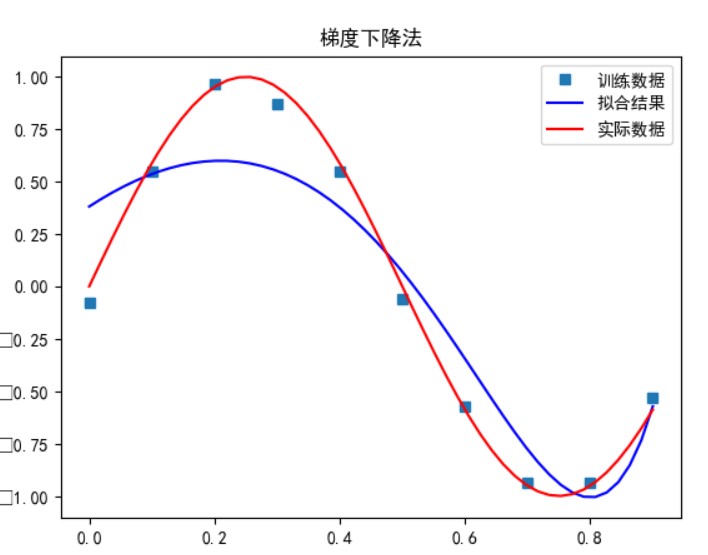
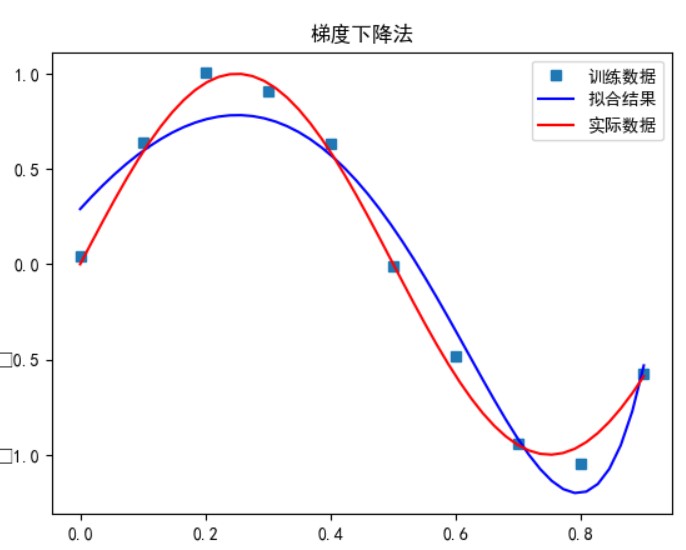
- 优化方法求解最优解(梯度下降,共轭梯度)
梯度下降法:
共轭梯度法:
- 用你得到的实验数据,解释过拟合。
多项式次数为 1 时:
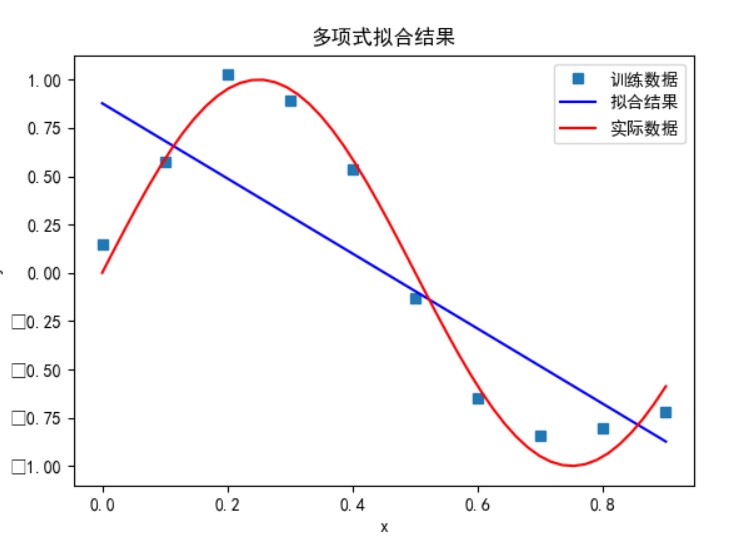
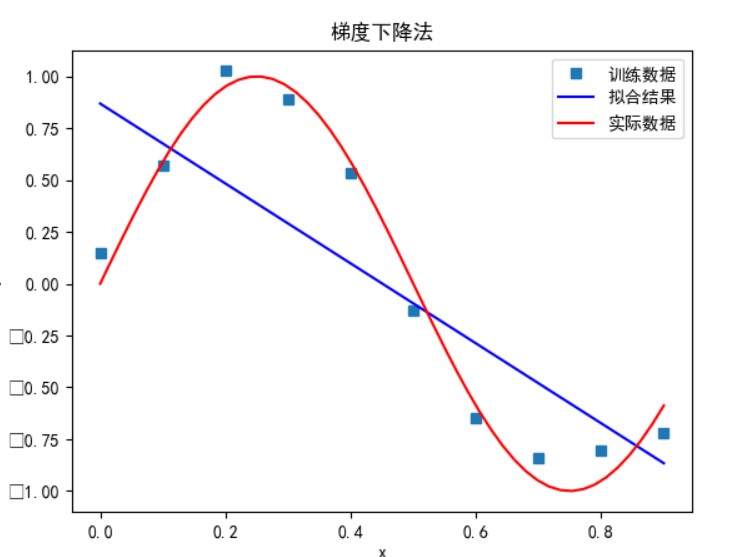
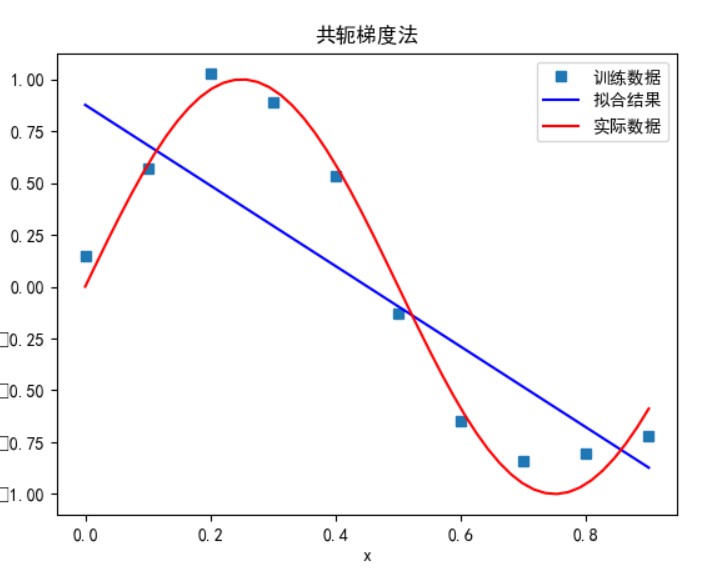
多项式次数为 3 时:

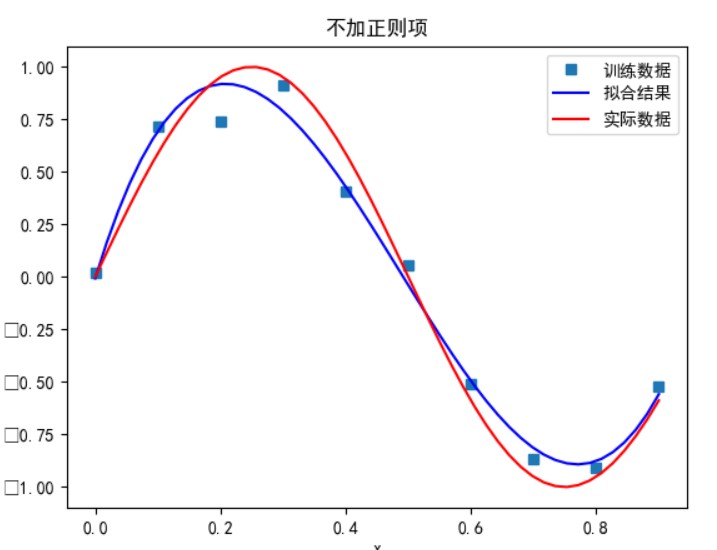
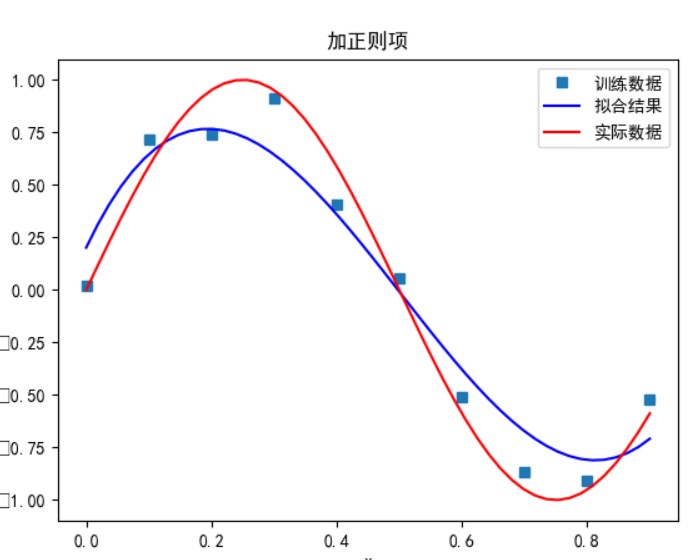
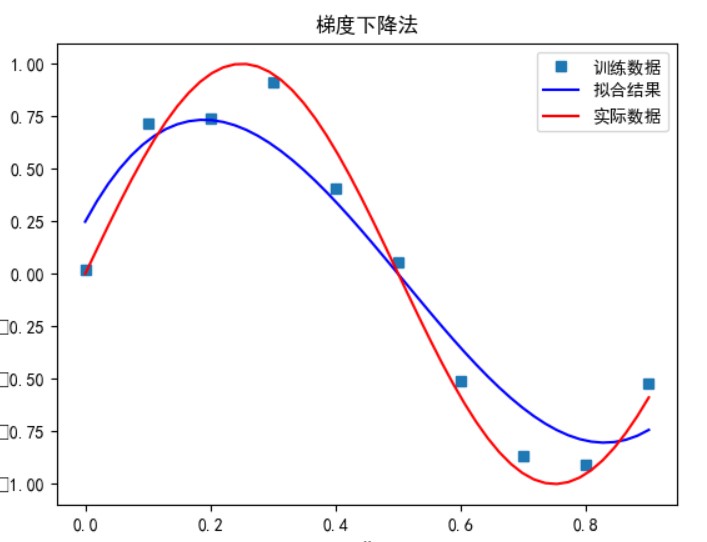
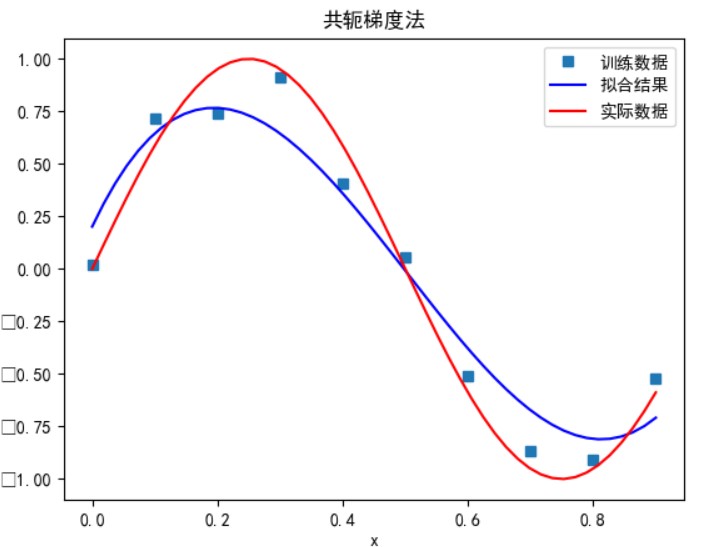
当多项式次数为 5 时:
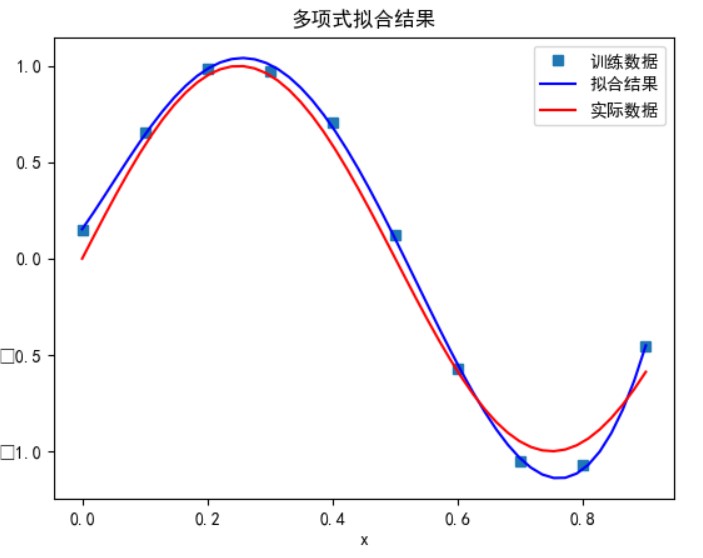
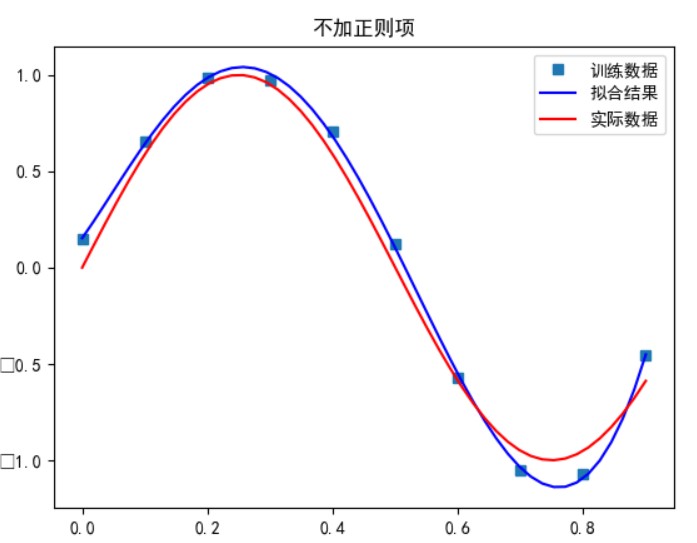
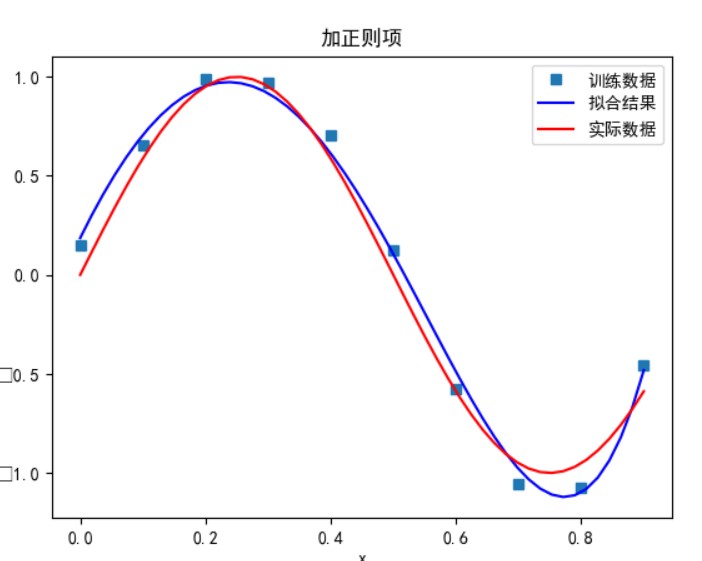
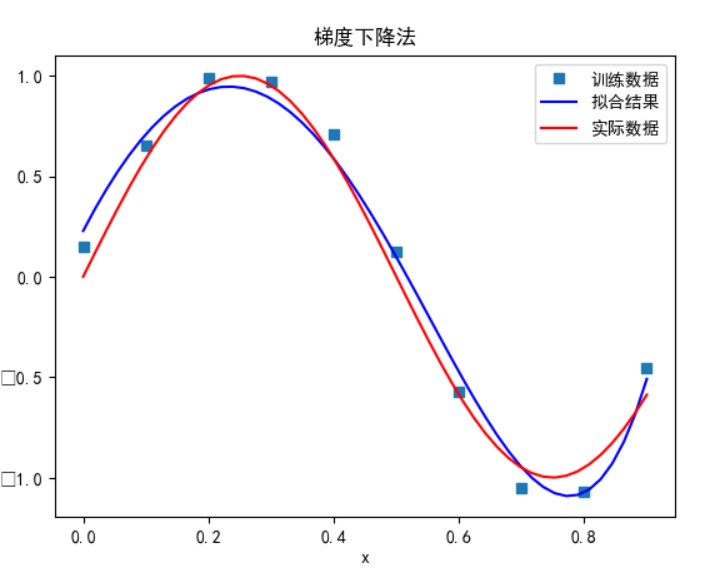
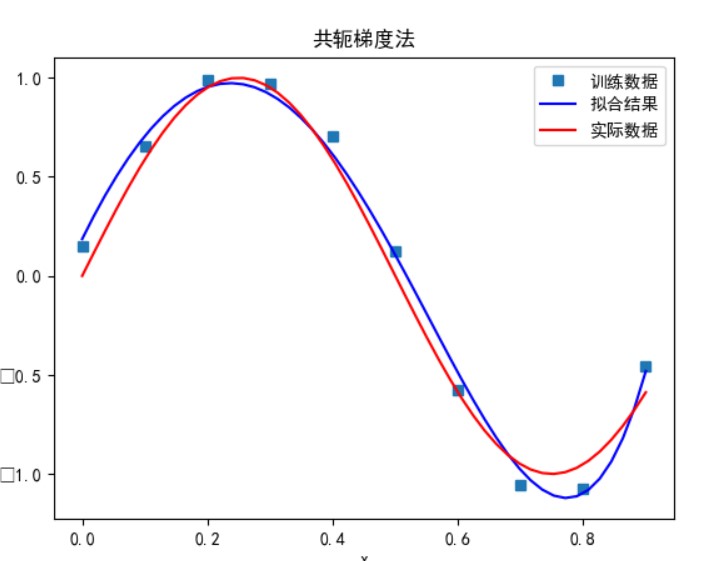
当多项式次数为 7 时:
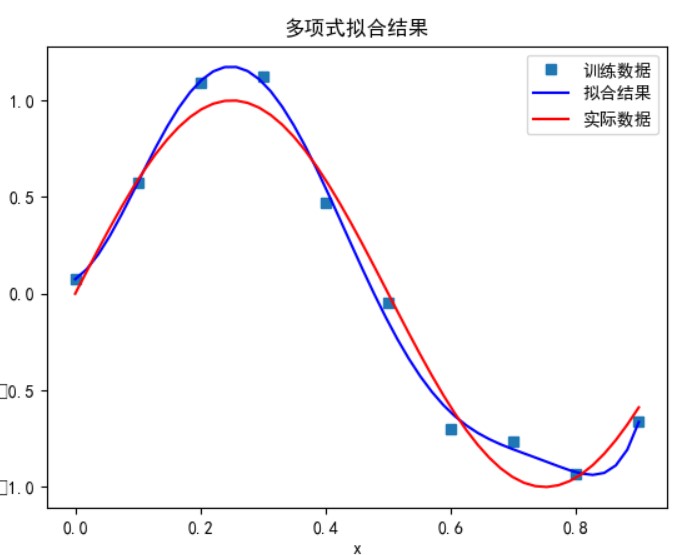
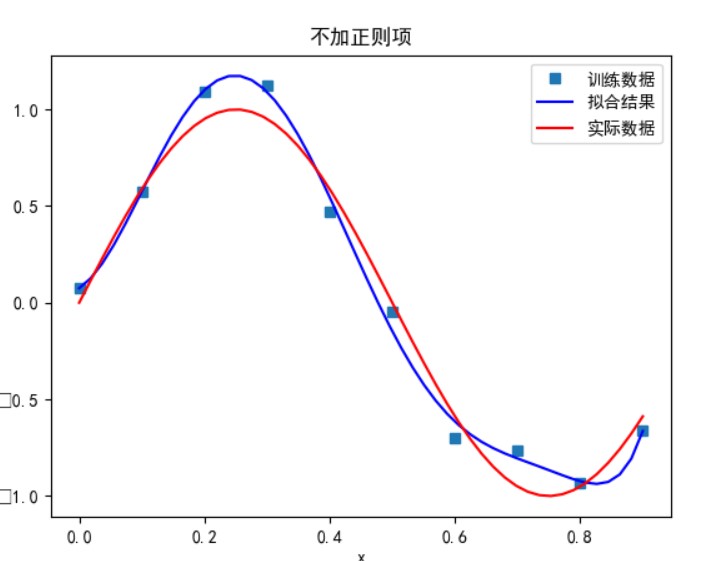
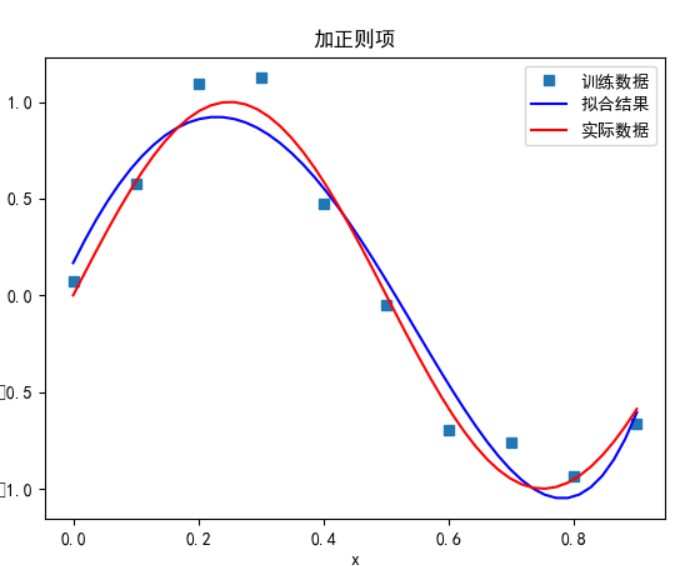
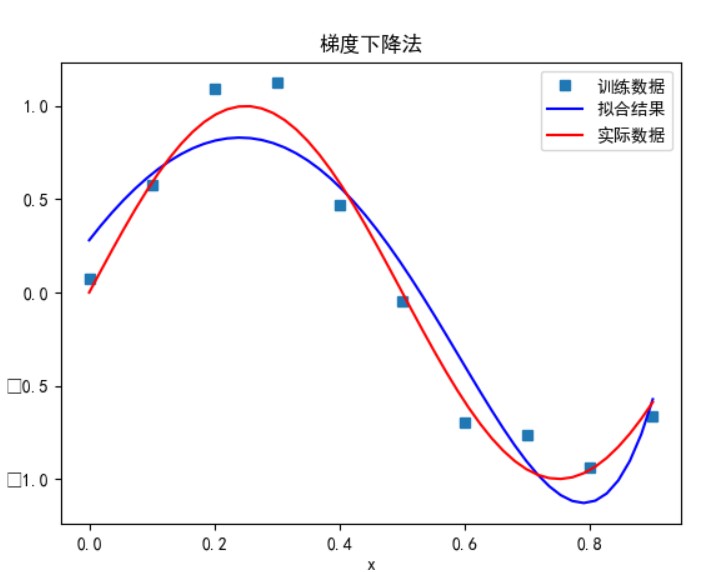
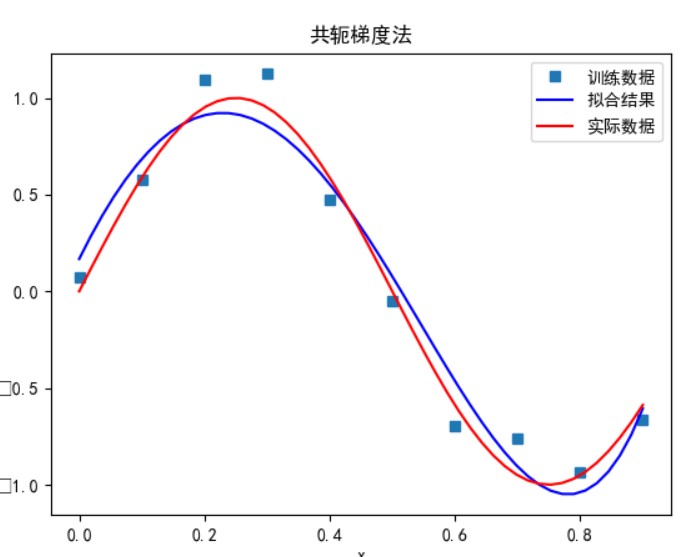
当多项式次数为 9 时:
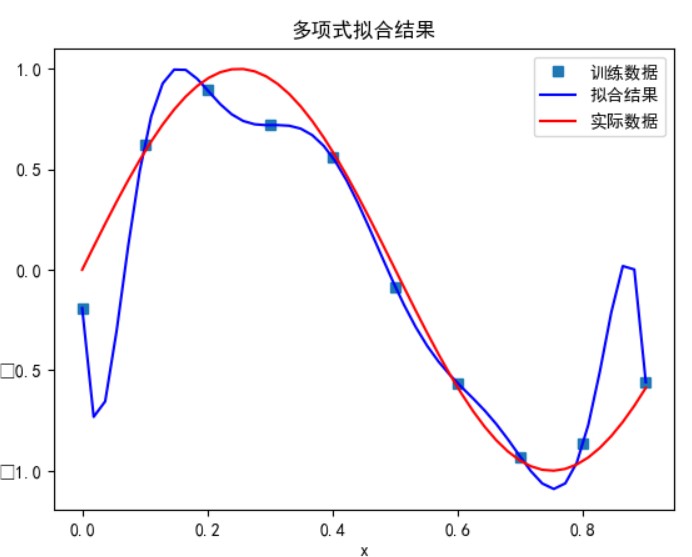
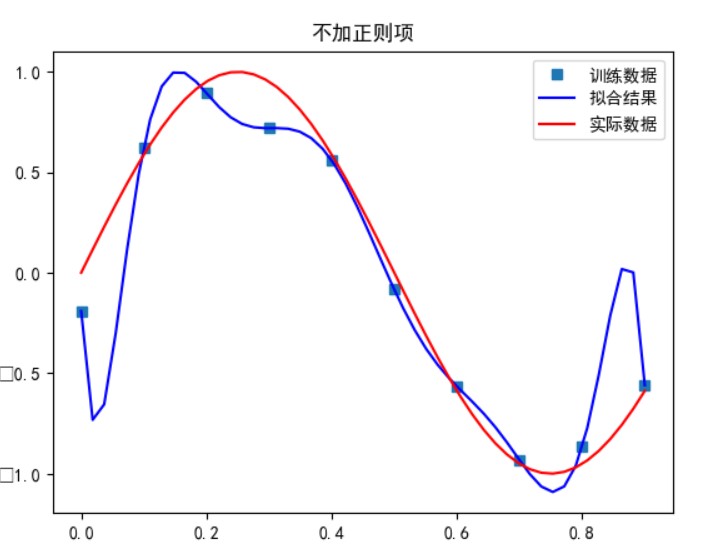
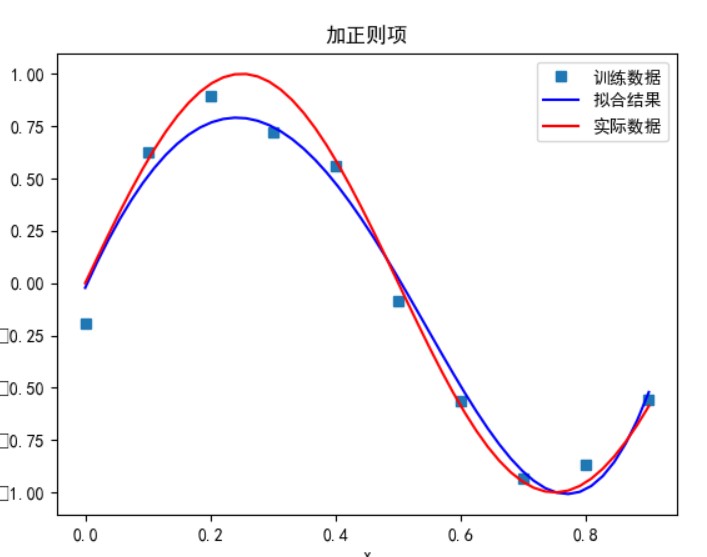
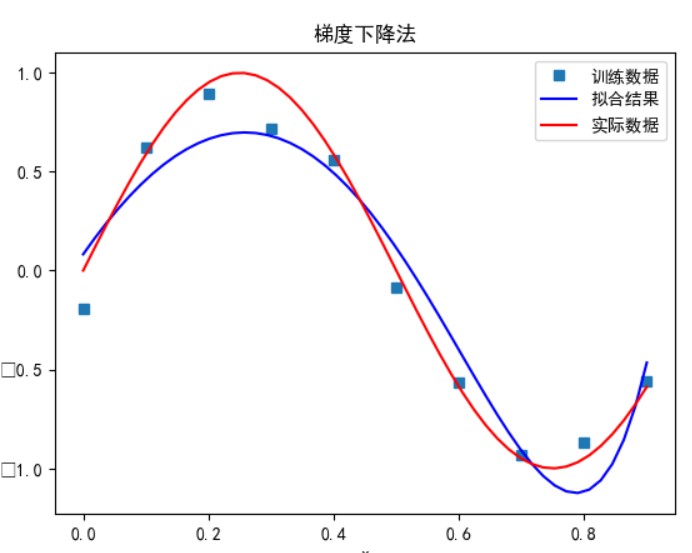
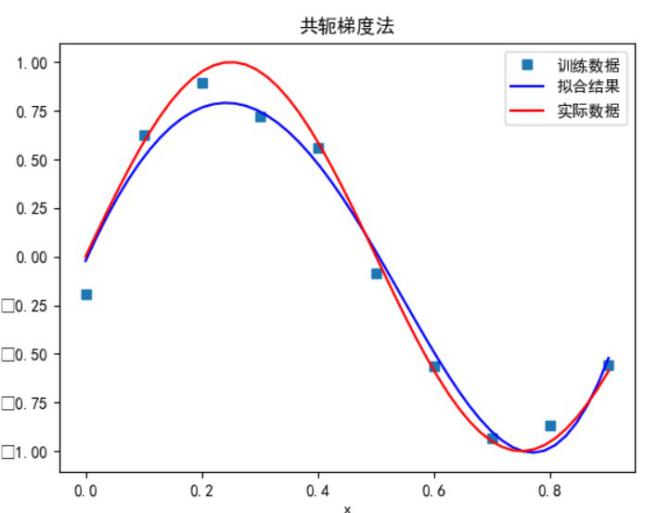
可以看到,多项式次数并不是越高拟合的效果就越好。
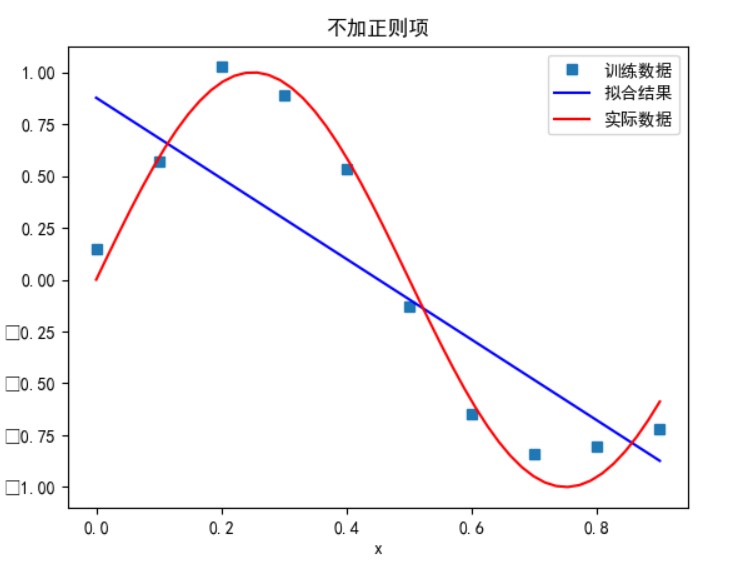
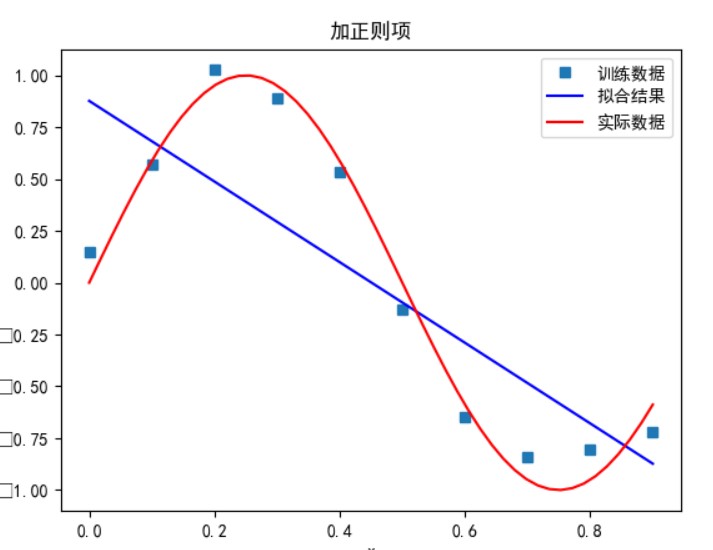
次数太小时无法正确拟合,次数在 5 时拟合的效果比较好,但再之后多项式次数过大时拟合的效果反而会变差,也就是出现了过拟合的情形。过拟合是由于样本数量过少,模型能力过强导致的。此时如果没有采用加入正则项等优化处理时拟合效果会非常差。
- 用不同数据量,不同超参数,不同的多项式阶数,比较实验效果。
数据量为 20,多项式次数为 9,超参数为 0.0001 时:
数据量为 30,多项式次数为 9,超参数为 0.0001 时:
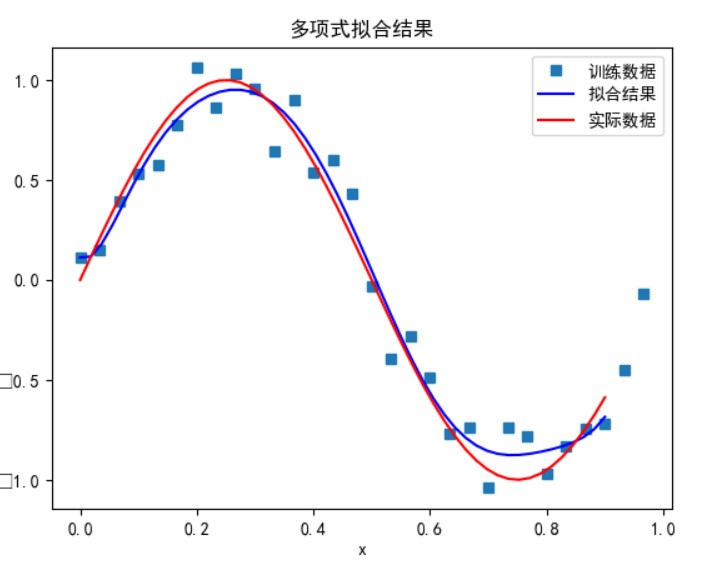
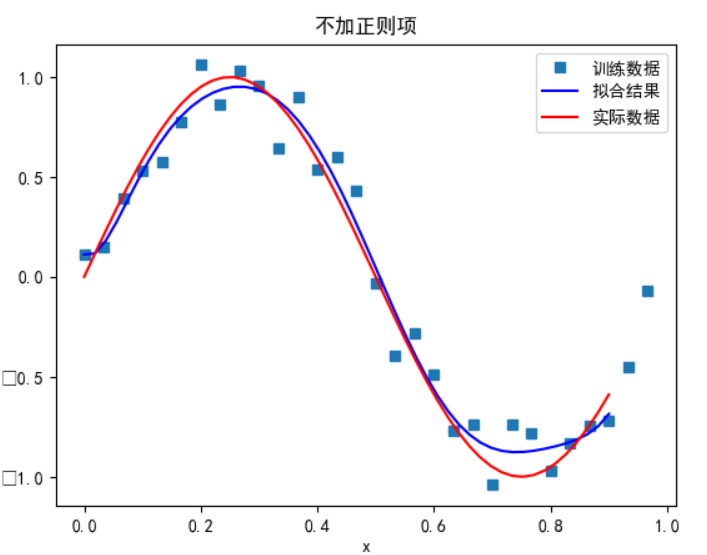
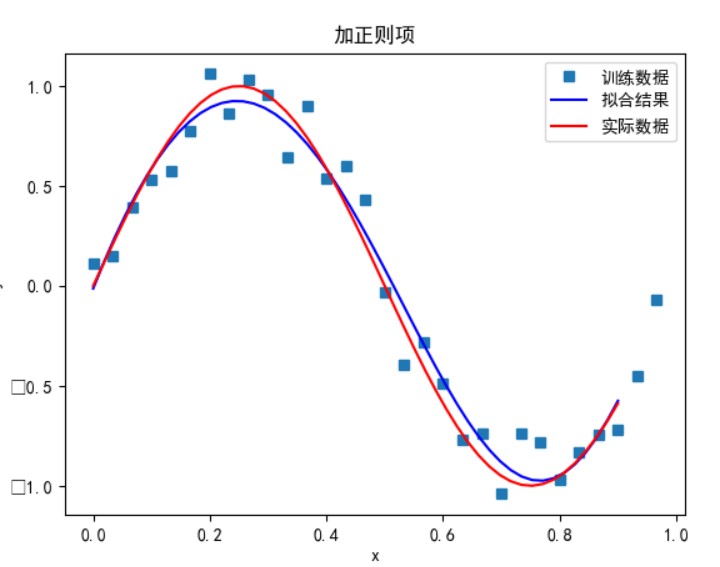
数据量为 40,多项式次数为 9,超参数为 0.0001 时:
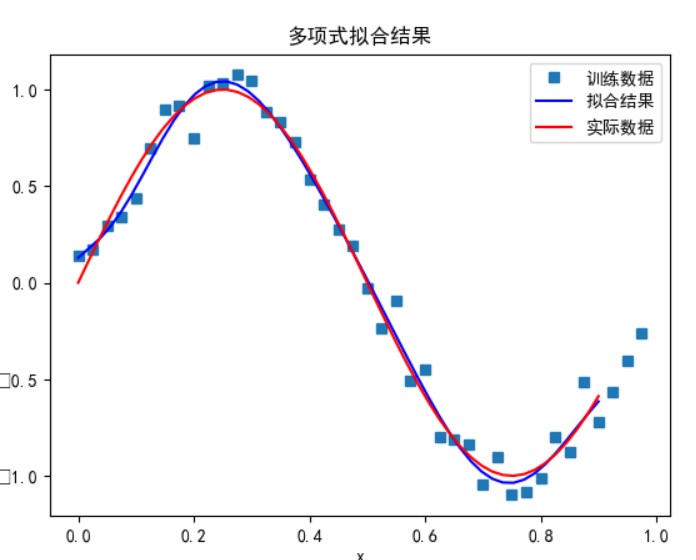
可以看到,相同条件下样本数据越多,拟合效果越好
数据量为 40,多项式次数为 9,超参数为 0.01 时:
数据量为 40,多项式次数为 9,超参数为 0.001 时:
数据量为 40,多项式次数为 9,超参数为 0.0001 时:
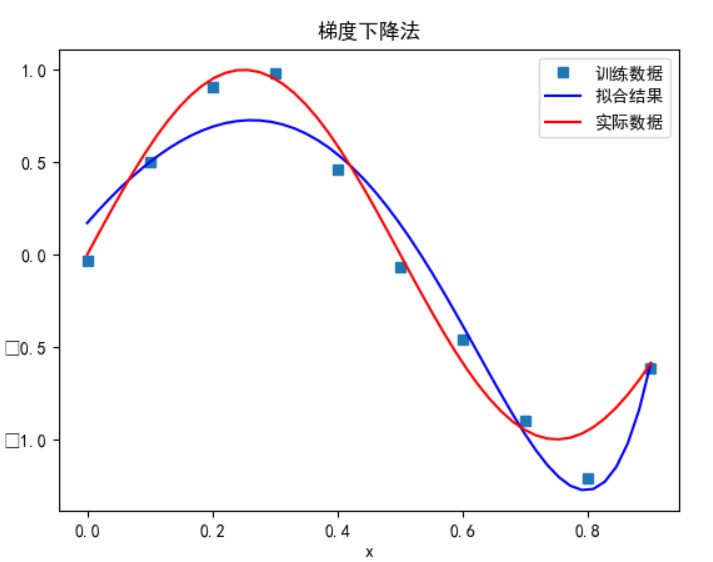
可以看到超参数对拟合效果影响很有限
参考文献
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于SSH架构的个人空间交友网站的设计与实现(北京邮电大学·隋昕航)
- 基于Java和Matlab的虚拟仿真实验系统的设计与实现(长江大学·喻盼)
- 基于Q-learning的系统集成与过程优化(青岛科技大学·魏晓彤)
- 中学python课程知识图谱构建及应用研究(华中师范大学·黄健)
- 基于Django的测试工具平台的设计与实现(北京交通大学·尚洁)
- 基于函数拟合的推荐算法改进研究(大连交通大学·苗子宇)
- 基于J2EE网络考试系统的设计与实现(吉林大学·叶丽娜)
- 基于SSH的教学效果评价系统的设计与实现(吉林大学·文胡)
- 复杂电磁环境信号生成及其软件设计(杭州电子科技大学·王雅)
- 基于Actor模型的广域分布式爬虫的设计与实现(北京邮电大学·陈凌鹏)
- 基于J2EE/SSH在线代码评测系统的设计与实现(电子科技大学·陈元静)
- 股票在线虚拟交易系统的设计与实现(电子科技大学·苏璇)
- 中学在线考试系统设计与实现(南京理工大学·周静)
- 基于Python的虚拟仪器设计与开发(中央民族大学·郑可富)
本文内容包括但不限于文字、数据、图表及超链接等)均来源于该信息及资料的相关主题。发布者:源码货栈 ,原文地址:https://bishedaima.com/yuanma/36152.html